기울기 (벡터 연산자)
둘러보기로 가기
검색하러 가기
맥스웰이 고안한 유체 시스템의 압력과 힘 사이의 관계는 ‘기울기’라는 벡터 연산자를 이용하면 간단하게 표현된다. 만약 어떤 지점 의 압력이 라는 함수에 의해 주어진 경우, 우리는 그 함수값들을 각 지점의 높이로 가지는 지형을 상상할 수 있다. 각 지점의 압력의 기울기는 그 지형상에서 위를 바라보았을 때 경사가 가장 가파른 방향과 그 경사의 크기를 나타내며, 수학적인 기호를 사용하면 다음과 같이 정의된다.
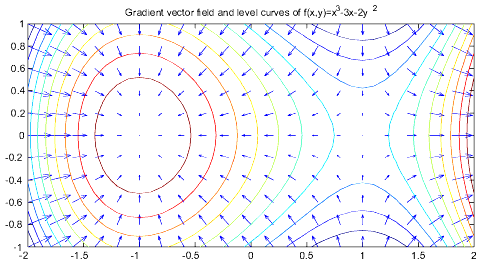
만약 지형이 일정한 고도 간격의 등고선이 그려진 아래와 같은 그림으로 주어질 경우, 기울기 벡터는 직관적인 방식으로도 구할 수 있다. 즉 각 지점의 기울기 벡터의 방향은 등고선에 수직이 되며, 기울기 벡터의 크기는 등고선의 간격에 반비례한다. 이러한 결과는 그림 속 화살표의 방향과 크기로 표시되어 있다. 만약 그림에 그려진 등고선들을 유체 시스템의 등압선들로 해석할 경우, 각 지점의 유체가 받는 힘은 라는 맥스웰의 공식에 의해 그림 속 화살표의 정반대가 된다.
관련 항목
- 발산 (벡터 연산자)
- 회전 (벡터 연산자)
- 정동욱, 뉴턴의 품에 들어온 힘의 선 (『패러데이 & 맥스웰』, 만남 4}}