대심과 투시 커플의 관계
정동욱, 정원호, 「위기 없는 혁명: 코페르니쿠스 혁명을 중심으로」, 『과학철학』 23권 2호 (2020), 1-51쪽 중 45-46쪽.
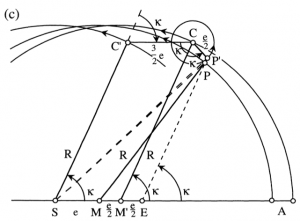
고대부터 행성 운동의 불규칙성은 태양과 무관한 1차 불규칙성과 태양과 관련된 2차 불규칙성으로 구분되어 분석되었다. 행성 운동의 2차 불규칙성이란 태양과 관련된 불규칙성을 의미하며, 흔히 행성의 ‘역행 운동’으로 대표되는 행성 운동의 불규칙성을 의미하며, 프톨레마이오스 체계에서 2차 불규칙성은 주원-주전원 체계를 통해 해결되었다(부록 1). 행성 운동의 1차 불규칙성이란 주원-주전원 체계를 도입하고서도 여전히 남는 오차를 의미하며, 프톨레마이오스 체계에서 1차 불규칙성은 이심(eccentric)과 대심(equant) 모형을 통해 해결되었다. 코페르니쿠스 체계에서는 2차 불규칙성은 태양 중심의 체계로 해결되었고, 1차 불규칙성은 이심과 투시 커플(Tusi couple)이라는 2개의 미세 주전원을 도입함으로써 해결되었다. 행성 운동의 2차 불규칙성만을 고려할 경우, 프톨레마이오스 체계와 코페르니쿠스 체계는 완벽하게 동일한 경험적 귀결을 가지며(부록 1), 1차 불규칙성에 대해 두 체계는 맨 눈을 이용한 관측을 통해서는 분간할 수 없는 매우 작은 차이만을 산출한다. 그림 5를 보자.
프톨레마이오스 체계에서 지구는 R의 반지름을 가진 행성의 주원의 중심 M이 아니라 그로부터 e만큼 벗어난 지점 S에 위치하며, 대심은 M으로부터 e만큼 떨어진 반대 지점 E에 위치한다. 주전원의 중심 P는 M을 중심으로 한 주원을 따라 돌지만, 대심 E를 기준으로 한 각속도, 즉 ∠PEA의 증가 속도가 ω로 일정하다. 따라서 P는 A 부근에서는 느리고 반대편에서는 빨라진다. 프톨레마이오스는 이러한 도구를 이용해 행성의 속도 변화를 상당히 성공적으로 예측할 수 있었다.
코페르니쿠스 체계에서 C′은 태양 S를 중심으로 한 반지름 R의 원주를 따라 각속도 ω로 돈다. 그리고 C는 C′을 중심으로 한 반지름 의 원을 따라 각속도 -ω로 돈다. 그러면 SM′CC′은 항상 평행사변형을 이룬다. 이제 행성 P′은 C를 중심으로 한 반지름 의 원을 따라 각속도 -2ω로 돈다. 그러면 행성 P′은 항상 직선 EP에서 P보다 살짝 위에 위치하게 되어, 결국 프톨레마이오스 체계에서 예측되는 행성의 위치와 매우 흡사한 위치에 있다.