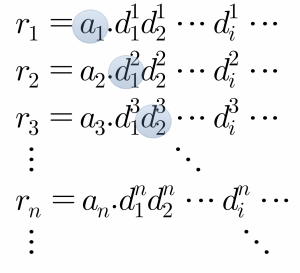"칸토어와 무한 집합"의 두 판 사이의 차이
(새 문서: 집합의 크기를 비교할 수 있으려면 무엇이 필요할까? 독일의 수학자 칸토어는 집합을 구성하는 원소들의 개수를 셀 수 없더라도 집합의...) |
|||
| 7번째 줄: | 7번째 줄: | ||
칸토어는 이러한 귀결을 확장하여, 자연수의 집합과 일대일 대응이 되는 무한 집합들을 ‘나열할 수 있는 무한 집합’으로 정의했다. 이에는 짝수의 집합, 홀수의 집합 등이 포함된다. 즉 이 무한 집합들은 모두 자연수의 집합과 크기가 같으며, 원소들을 빠짐없이 일렬로 나열할 수 있는 방법이 존재한다. 그러나 자연수의 집합과 일대일 대응이 될 수 없는 무한 집합도 존재했는데, 이들은 ‘나열할 수 없는 무한 집합’으로 정의되었다. | 칸토어는 이러한 귀결을 확장하여, 자연수의 집합과 일대일 대응이 되는 무한 집합들을 ‘나열할 수 있는 무한 집합’으로 정의했다. 이에는 짝수의 집합, 홀수의 집합 등이 포함된다. 즉 이 무한 집합들은 모두 자연수의 집합과 크기가 같으며, 원소들을 빠짐없이 일렬로 나열할 수 있는 방법이 존재한다. 그러나 자연수의 집합과 일대일 대응이 될 수 없는 무한 집합도 존재했는데, 이들은 ‘나열할 수 없는 무한 집합’으로 정의되었다. | ||
[[파일:칸토어의 대각선 논증.png|대체글=칸토어의 대각선 논증|섬네일|그림. 칸토어의 대각선 논증]] | [[파일:칸토어의 대각선 논증.png|대체글=칸토어의 대각선 논증|섬네일|그림. 칸토어의 대각선 논증]] | ||
칸토어는 ‘대각선 논증’이란 방법을 이용하여 실수의 집합이 자연수의 집합보다 큰 ‘나열할 수 없는 무한 집합’임을 증명했다. 우선 실수를 그림과 같이 자연수와 일대일 대응시키는 방법이 있다고 가정해 보자(단, <math>a</math>는 실수의 정수부, <math>d_i</math>는 실수의 소수점아래 <math>i</math>번째 수). 이러한 나열에서 <math>r_1</math>은 자연수 1과 대응되는 실수이고, <math>r_2</math>는 자연수 2와 대응되는 실수이며, 자연수 <math>n</math>과 대응되는 실수는 <math>r_n = a_n . d_1^n d_2^n \cdots d_i^n \cdots </math>이 된다. 만약 자연수와의 대응이 완벽하다면, 모든 실수는 이런 방식에 의해 빠짐없이 나열될 수 있을 것이다. 그러나 위와 같은 나열이 완성되었다고 할 때, 우리는 나열된 어떤 수와도 다른 수를 언제나 생각해낼 수 있다. 예를 들어, 정수부의 수는 <math>a_1</math>과 다르고, 소수점아래 첫째 자리의 수는 <math>d_1^2</math>와 다르고, 소수점아래 둘째 자리의 수는 <math>d_2^3</math>과 다르고, 이런 방식으로 계속 대각선을 따라 소수점아래 번째 자리의 수를 <math>d_i^{i+1}</math>과 다르도록 수를 만든다면, 그 수는 나열된 어떤 수와도 다른 새로운 실수가 된다. 이는 실수를 빠짐없이 자연수와 대응시킬 수 있다는 가정이 잘못되었음을 말해준다. 즉 실수의 집합은 자연수의 집합보다 크기가 큰 것이다. | 칸토어는 ‘대각선 논증’이란 방법을 이용하여 실수의 집합이 자연수의 집합보다 큰 ‘나열할 수 없는 무한 집합’임을 증명했다. 우선 실수를 그림과 같이 자연수와 일대일 대응시키는 방법이 있다고 가정해 보자(단, <math>a</math>는 실수의 정수부, <math>d_i</math>는 실수의 소수점아래 <math>i</math>번째 수). 이러한 나열에서 <math>r_1</math>은 자연수 1과 대응되는 실수이고, <math>r_2</math>는 자연수 2와 대응되는 실수이며, 자연수 <math>n</math>과 대응되는 실수는 <math>r_n = a_n . d_1^n d_2^n \cdots d_i^n \cdots </math>이 된다. 만약 자연수와의 대응이 완벽하다면, 모든 실수는 이런 방식에 의해 빠짐없이 나열될 수 있을 것이다. 그러나 위와 같은 나열이 완성되었다고 할 때, 우리는 나열된 어떤 수와도 다른 수를 언제나 생각해낼 수 있다. 예를 들어, 정수부의 수는 <math>a_1</math>과 다르고, 소수점아래 첫째 자리의 수는 <math>d_1^2</math>와 다르고, 소수점아래 둘째 자리의 수는 <math>d_2^3</math>과 다르고, 이런 방식으로 계속 대각선을 따라 소수점아래 <math>i</math>번째 자리의 수를 <math>d_i^{i+1}</math>과 다르도록 수를 만든다면, 그 수는 나열된 어떤 수와도 다른 새로운 실수가 된다. 이는 실수를 빠짐없이 자연수와 대응시킬 수 있다는 가정이 잘못되었음을 말해준다. 즉 실수의 집합은 자연수의 집합보다 크기가 큰 것이다. | ||
무한 집합의 크기에 대한 칸토어의 제안들은 그 당시에는 쉽게 받아들여지지 않았지만, 결국에는 현대 수학의 핵심적인 분야 중 하나인 집합론의 확고한 기초로서 자리잡게 된다. | 무한 집합의 크기에 대한 칸토어의 제안들은 그 당시에는 쉽게 받아들여지지 않았지만, 결국에는 현대 수학의 핵심적인 분야 중 하나인 집합론의 확고한 기초로서 자리잡게 된다. | ||
2025년 9월 3일 (수) 09:55 기준 최신판
집합의 크기를 비교할 수 있으려면 무엇이 필요할까? 독일의 수학자 칸토어는 집합을 구성하는 원소들의 개수를 셀 수 없더라도 집합의 크기를 비교할 수 있다고 제안한다. 그에 따르면, 두 집합의 사이에 일대일 대응이 가능하면 두 집합은 크기가 같다. 그러나 만약 집합 A가 집합 B의 부분집합과 일대일 대응되는 반면 집합 B는 집합 A의 부분집합과 일대일 대응될 수 없다면, 집합 A는 집합 B보다 크기가 크다.
칸토어가 제안한 방법은 상식적인 직관을 사용하고 있다. 예를 들어, 집합 {1,2,3}과 집합 {4,5,6}의 크기를 비교하고자 할 경우, 우리는 1과 4를 짝짓고, 2와 5를 짝짓고, 3과 6을 짝지은 후 양 집합에 더 이상 남는 원소가 없다는 것을 확인함으로써 두 집합의 크기가 같다는 것을 알 수 있다. 두 집합이 각각 3개의 원소로 이루어졌다는 것은 꼭 알 필요가 없는 것이다.
칸토어의 방법은 원소의 개수를 셀 필요가 없기 때문에 무한 집합의 크기를 비교하는 데도 적용될 수 있다. 예를 들어 자연수의 집합과 짝수의 집합의 크기를 비교한다면 어떻게 될까? 모든 짝수는 자연수에 포함되지만, 자연수에는 짝수가 아닌 홀수도 포함되어 있다. 따라서 자연수의 집합은 짝수의 집합보다 크기가 커 보인다. 그러나 자연수 집합의 n을 짝수 집합의 2n과 대응시키는 방법을 사용할 경우, 우리는 두 집합을 정확하게 일대일 대응시킬 수 있다. 즉 자연수의 집합과 짝수의 집합은 크기가 같다는 결론이 따라 나온다.
칸토어는 이러한 귀결을 확장하여, 자연수의 집합과 일대일 대응이 되는 무한 집합들을 ‘나열할 수 있는 무한 집합’으로 정의했다. 이에는 짝수의 집합, 홀수의 집합 등이 포함된다. 즉 이 무한 집합들은 모두 자연수의 집합과 크기가 같으며, 원소들을 빠짐없이 일렬로 나열할 수 있는 방법이 존재한다. 그러나 자연수의 집합과 일대일 대응이 될 수 없는 무한 집합도 존재했는데, 이들은 ‘나열할 수 없는 무한 집합’으로 정의되었다.
칸토어는 ‘대각선 논증’이란 방법을 이용하여 실수의 집합이 자연수의 집합보다 큰 ‘나열할 수 없는 무한 집합’임을 증명했다. 우선 실수를 그림과 같이 자연수와 일대일 대응시키는 방법이 있다고 가정해 보자(단, 는 실수의 정수부, 는 실수의 소수점아래 번째 수). 이러한 나열에서 은 자연수 1과 대응되는 실수이고, 는 자연수 2와 대응되는 실수이며, 자연수 과 대응되는 실수는 이 된다. 만약 자연수와의 대응이 완벽하다면, 모든 실수는 이런 방식에 의해 빠짐없이 나열될 수 있을 것이다. 그러나 위와 같은 나열이 완성되었다고 할 때, 우리는 나열된 어떤 수와도 다른 수를 언제나 생각해낼 수 있다. 예를 들어, 정수부의 수는 과 다르고, 소수점아래 첫째 자리의 수는 와 다르고, 소수점아래 둘째 자리의 수는 과 다르고, 이런 방식으로 계속 대각선을 따라 소수점아래 번째 자리의 수를 과 다르도록 수를 만든다면, 그 수는 나열된 어떤 수와도 다른 새로운 실수가 된다. 이는 실수를 빠짐없이 자연수와 대응시킬 수 있다는 가정이 잘못되었음을 말해준다. 즉 실수의 집합은 자연수의 집합보다 크기가 큰 것이다.
무한 집합의 크기에 대한 칸토어의 제안들은 그 당시에는 쉽게 받아들여지지 않았지만, 결국에는 현대 수학의 핵심적인 분야 중 하나인 집합론의 확고한 기초로서 자리잡게 된다.