"에테르와 상대성 이론"의 두 판 사이의 차이
| 1번째 줄: | 1번째 줄: | ||
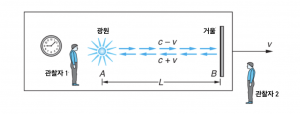
19세기 물리학자인 마이켈슨과 몰리는 지구의 절대 운동에 따른 효과를 탐지하고자 했다. 그들이 가정한 에테르 이론에 따르면, 우주는 ‘에테르’라는 매질로 가득 채워져 있으며, 빛은 에테르의 진동을 통해 전달되는 파동이다. 또한 에테르는 절대 공간에 고정되어 있기에 운동의 절대적 기준이 된다고 가정되었다. 그렇다면 에테르를 기준으로 관찰자-광원-거울이 함께 <math>v</math>의 속도로 운동 중인 그림 1의 시스템을 상상해 보자. | 19세기 물리학자인 마이켈슨과 몰리는 지구의 절대 운동에 따른 효과를 탐지하고자 했다. 그들이 가정한 에테르 이론에 따르면, 우주는 ‘에테르’라는 매질로 가득 채워져 있으며, 빛은 에테르의 진동을 통해 전달되는 파동이다. 또한 에테르는 절대 공간에 고정되어 있기에 운동의 절대적 기준이 된다고 가정되었다. 그렇다면 에테르를 기준으로 관찰자-광원-거울이 함께 <math>v</math>의 속도로 운동 중인 그림 1의 시스템을 상상해 보자. | ||
[[그림:그림 1. 에테르에 대해 v의 속도로 함께 운동 중인 관찰자-광원-거울 시스템.png|thumb|그림 1. 에테르에 대해 v의 속도로 함께 운동 중인 관찰자-광원-거울 시스템]]파동인 빛의 전파 속도는 에테르에 대해 <math>c</math>로 일정하므로, 에테르에 대해 정지한 관찰자 2에게 빛의 속도는 <math>c</math>로 일정하다. 따라서 A(광원)에서 출발한 빛은 <math>\frac{L}{c-v}</math>의 시간 동안 <math>\frac{L}{1-v/c}</math>의 거리를 이동하여 B(거울)에 도달하고, B에서 반사된 빛은 <math>\frac{L}{c+v}</math>의 시간 동안 <math>\frac{L}{1+v/c}</math>의 거리를 이동하여 A(관찰자)에 도달한다. 이를 운동 중인 시스템 내의 관찰자 1의 관점에서 보면, 빛은 A에서 B까지 <math>c-v</math>의 속도로 거리 <math>L</math>을 이동하고, B에서 A까지 <math>c+v</math>의 속도로 다시 거리 <math>L</math>을 이동한다. 즉 그에게 빛이 AB를 왕복하는 평균 속도는 빛의 이동 거리 <math>2L</math>을 이동 시간 <math>\frac{L}{c-v} + \frac{L}{c+v}</math>, 즉 <math>\frac{2L}{c \ | [[그림:그림 1. 에테르에 대해 v의 속도로 함께 운동 중인 관찰자-광원-거울 시스템.png|thumb|그림 1. 에테르에 대해 v의 속도로 함께 운동 중인 관찰자-광원-거울 시스템]]파동인 빛의 전파 속도는 에테르에 대해 <math>c</math>로 일정하므로, 에테르에 대해 정지한 관찰자 2에게 빛의 속도는 <math>c</math>로 일정하다. 따라서 A(광원)에서 출발한 빛은 <math>\frac{L}{c-v}</math>의 시간 동안 <math>\frac{L}{1-v/c}</math>의 거리를 이동하여 B(거울)에 도달하고, B에서 반사된 빛은 <math>\frac{L}{c+v}</math>의 시간 동안 <math>\frac{L}{1+v/c}</math>의 거리를 이동하여 A(관찰자)에 도달한다. 이를 운동 중인 시스템 내의 관찰자 1의 관점에서 보면, 빛은 A에서 B까지 <math>c-v</math>의 속도로 거리 <math>L</math>을 이동하고, B에서 A까지 <math>c+v</math>의 속도로 다시 거리 <math>L</math>을 이동한다. 즉 그에게 빛이 AB를 왕복하는 평균 속도는 빛의 이동 거리 <math>2L</math>을 이동 시간 <math>\frac{L}{c-v} + \frac{L}{c+v}</math>, 즉 <math>\frac{2L}{c \{ 1-(v/c)^{2} \}}</math>로 나눈 값인 <math>c \{ 1- ( v/c )^{2} \}</math>으로, 이를 실험을 통해 측정한다면 에테르에 대한 시스템의 속도인 <math>v</math>의 값에 따라 달라져야 한다. 그런데 지구는 자전과 공전을 하므로, 에테르를 기준으로 한 지표면의 운동은 1일 및 1년 주기의 변화를 겪을 것이고, 따라서 지구상에서 측정되는 빛의 평균 속도 역시 주기적으로 달라질 것이다. 그러나 그러한 주기적 변화는 어떠한 측정 장치로도 탐지되지 않았다. | ||
결국 에테르 이론에 기초하여 지구의 절대 운동을 탐지하려는 마이켈슨과 몰리의 계획은 실패했다. 대다수의 과학자들은 여전히 에테르 이론에 기초하여 왜 빛의 속도가 관찰자의 운동과 무관하게 일정한 것처럼 측정되는지를 설명하기 위해 노력했다. 그러나 아인슈타인은 에테르가 없기에 에테르에 대한 관찰자의 운동은 어떠한 방법으로도 탐지될 수 없다고 생각했다. 그는 관찰자의 운동과 무관하게 빛의 속도가 <math>c</math>로 언제나 일정하다는 광속 불변의 원리를 참으로 전제한 후, 관찰자에 따라 시간이 다르게 흐를 수 있다고 주장했다. 나의 1초는 다른 누군가의 1초와 다를 수 있다는 것이다. | 결국 에테르 이론에 기초하여 지구의 절대 운동을 탐지하려는 마이켈슨과 몰리의 계획은 실패했다. 대다수의 과학자들은 여전히 에테르 이론에 기초하여 왜 빛의 속도가 관찰자의 운동과 무관하게 일정한 것처럼 측정되는지를 설명하기 위해 노력했다. 그러나 아인슈타인은 에테르가 없기에 에테르에 대한 관찰자의 운동은 어떠한 방법으로도 탐지될 수 없다고 생각했다. 그는 관찰자의 운동과 무관하게 빛의 속도가 <math>c</math>로 언제나 일정하다는 광속 불변의 원리를 참으로 전제한 후, 관찰자에 따라 시간이 다르게 흐를 수 있다고 주장했다. 나의 1초는 다른 누군가의 1초와 다를 수 있다는 것이다. | ||
2022년 11월 8일 (화) 23:39 판
19세기 물리학자인 마이켈슨과 몰리는 지구의 절대 운동에 따른 효과를 탐지하고자 했다. 그들이 가정한 에테르 이론에 따르면, 우주는 ‘에테르’라는 매질로 가득 채워져 있으며, 빛은 에테르의 진동을 통해 전달되는 파동이다. 또한 에테르는 절대 공간에 고정되어 있기에 운동의 절대적 기준이 된다고 가정되었다. 그렇다면 에테르를 기준으로 관찰자-광원-거울이 함께 의 속도로 운동 중인 그림 1의 시스템을 상상해 보자.
파동인 빛의 전파 속도는 에테르에 대해 로 일정하므로, 에테르에 대해 정지한 관찰자 2에게 빛의 속도는 로 일정하다. 따라서 A(광원)에서 출발한 빛은 의 시간 동안 의 거리를 이동하여 B(거울)에 도달하고, B에서 반사된 빛은 의 시간 동안 의 거리를 이동하여 A(관찰자)에 도달한다. 이를 운동 중인 시스템 내의 관찰자 1의 관점에서 보면, 빛은 A에서 B까지 의 속도로 거리 을 이동하고, B에서 A까지 의 속도로 다시 거리 을 이동한다. 즉 그에게 빛이 AB를 왕복하는 평균 속도는 빛의 이동 거리 을 이동 시간 , 즉 로 나눈 값인 으로, 이를 실험을 통해 측정한다면 에테르에 대한 시스템의 속도인 의 값에 따라 달라져야 한다. 그런데 지구는 자전과 공전을 하므로, 에테르를 기준으로 한 지표면의 운동은 1일 및 1년 주기의 변화를 겪을 것이고, 따라서 지구상에서 측정되는 빛의 평균 속도 역시 주기적으로 달라질 것이다. 그러나 그러한 주기적 변화는 어떠한 측정 장치로도 탐지되지 않았다.
결국 에테르 이론에 기초하여 지구의 절대 운동을 탐지하려는 마이켈슨과 몰리의 계획은 실패했다. 대다수의 과학자들은 여전히 에테르 이론에 기초하여 왜 빛의 속도가 관찰자의 운동과 무관하게 일정한 것처럼 측정되는지를 설명하기 위해 노력했다. 그러나 아인슈타인은 에테르가 없기에 에테르에 대한 관찰자의 운동은 어떠한 방법으로도 탐지될 수 없다고 생각했다. 그는 관찰자의 운동과 무관하게 빛의 속도가 로 언제나 일정하다는 광속 불변의 원리를 참으로 전제한 후, 관찰자에 따라 시간이 다르게 흐를 수 있다고 주장했다. 나의 1초는 다른 누군가의 1초와 다를 수 있다는 것이다.
[그림:그림 2. 에테르에 대해 (a) 도선이 고정된 채 자석이 접근하는 경우와 (b) 자석이 고정된 채 도선이 접근하는 경우.png|thumb|그림 2. 에테르에 대해 (a) 도선이 고정된 채 자석이 접근하는 경우와 (b) 자석이 고정된 채 도선이 접근하는 경우]]아인슈타인은 일찍이 고전 전자기학의 비대칭적 성격으로부터 에테르의 필요성을 의심하고 있었다. 고전 전자기학에 따르면, 전기장과 자기장은 에테르라는 매질의 서로 다른 상태들로, 자기장의 변화는 전기장을 낳으며, 전기장은 그곳에 놓인 도선에 전류를 흐르게 만든다. 그래서 그림 2a처럼 에테르에 대해 고정된 도선에 자석을 접근시키면 도선에 전류가 유도되는 것이다. 그런데 고전 전자기학에 따르면, 고정된 자기장 하에서 움직이는 전하는 특정한 방향의 힘을 받아 운동하게 된다. 그래서 그림 2b처럼 에테르에 대해 고정된 자석에 도선을 접근시키면 도선 속 전하들이 힘을 받아 전류가 유도되는 것이다. 결국 고전 전자기학은 그림 2의 두 현상을 서로 다른 에테르의 상태에서 비롯된 별개의 현상처럼 기술한다. 그림 2a에서는 전기장이 존재하는 반면 그림 2b에서는 전기장이 존재하지 않기 때문이다. 그러나 두 현상은 관찰을 통해 구분될 수 없다. 아인슈타인이 보기에, 두 현상은 자석과 도선의 상대적인 운동에 의해 회로에 전류가 유도되는 완벽하게 동일한 현상으로, 둘을 다른 현상처럼 기술하는 것은 에테르라는 고정된 매질을 가정함으로써 발생하는 착각인 것이다.
그렇다면 두 현상은 어떻게 동일한 방식으로 이해될 수 있을까? 아인슈타인에 따르면 자연에 실재하는 것은 전기장이나 자기장이 아니라 전자기장이며, 특정한 상태의 전자기장은 관찰자의 운동에 따라 전기장 성분과 자기장 성분으로 다르게 분해되어 관찰된다. 그래서 자석과 도선의 상대적인 운동에 의해 전류가 유도되는 동일한 현상은 서로 다른 관찰자에게 서로 다른 방식으로 관찰될 뿐이다. 즉 도선에 대해 정지해 있는 관찰자에게는 그림 2a에 대한 고전 전자기학의 기술처럼 전기장 성분이 탐지되고, 자석에 대해 정지해 있는 관찰자에게는 그림 2b에 대한 고전 전자기학의 기술처럼 전기장 성분이 탐지되지 않을 뿐, 전자기장의 측면에서는 동일한 일이 벌어진 것으로 이해될 수 있다는 것이다. 이러한 이해 방식에서는 전기장과 자기장을 관찰자와 무관한 방식으로 기술하기 위해 가정해야 했던 에테르라는 존재는 불필요해진다.