코페르니쿠스 체계의 조화와 증거

도입

코페르니쿠스는 『천구의 회전에 관하여』 1권 10장에서 자신의 태양 중심 체계 하에서는 지구 중심의 체계 하에서는 발견할 수 없는 “우주의 놀라운 대칭성과 … 천구의 운동과 크기 사이의 조화로운 관계를 발견”할 수 있다는 점을 강조하며 태양 중심 체계를 옹호했다. 이에 주목한 과학철학자 토머스 쿤은 코페르니쿠스의 “이러한 논증들은 기껏해야 실제 천문학자의 실용적 감각이 아닌 그의 미적 감각에만 호소력을 가질 뿐”(쿤 2016, 354쪽)이며 “천문학자들에게 코페르니쿠스 체계와 프톨레마이오스 체계 사이의 선택은 처음에는 단지 취향의 문제일 수 있었”(쿤 2016, 334쪽)다고 주장했다.

그러나 많은 학자들은 쿤의 주장에 의문을 품었다. 마르텐스(Martens 2009)는 통합성과 조화에 근거한 코페르니쿠스의 논변이 증거적 논변으로 의도되었다고 주장했으며, 글리모어(Glymour 1980, 6장), 포스터(Forster 2004), 소버(Sober 2015, 1장), 마이어볼트(Myrvold 2003) 등은 논리적, 확률적 분석을 통해 태양중심설의 이론적 통합성과 조화가 미적인 장점일 뿐 아니라 진정한 인식적 장점이라고 주장했다. 즉 코페르니쿠스가 내세운 태양중심설의 장점들은 평가자의 미적 취향이 달라지더라도 사라질 수 없는 비주관적인 인식적 장점이라는 것이다.

이 글에서는 우선 코페르니쿠스가 의도했던 태양 중심 체계의 놀라운 대칭성과 조화가 정확히 무엇인지 밝힌 후, 이러한 태양 중심 체계의 대칭성과 조화가 그 체계를 뒷받침하는 증거로 간주될 수 있었는지에 대해 검토할 것이다. 이러한 물음에 답하기 위해서는 우선 지구 중심의 프톨레마이오스 체계를 대면해야 한다.

행성의 운동과 프톨레마이오스 체계

그림 1. 별의 일주 운동

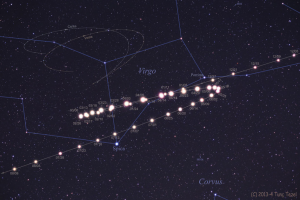
지구상의 관찰자의 입장에서 하늘에는 별(항성)과 행성이라는 두 가지 종류의 천체가 있다. 별들은 하루(정확히는 23시간 56분)에 한 바퀴씩 도는 일주 운동을 하며, 그들은 마치 하나의 판에 박혀 있는 것처럼 항상 단체로 움직인다(그림 1). 우리가 하늘에서 별자리를 알아볼 수 있는 것도 바로 그 덕분이다. 그래서 고대의 학자들은 그 별들이 하나의 항성 천구에 고정되어 있으며, 항성 천구의 회전을 통해 모든 별들이 함께 회전한다고 생각했다. 반면 태양, 달, 수성, 금성, 화성, 목성, 토성은 별들과 마찬가지로 매일 뜨고 지는 운동을 하면서도(일주 운동), 별자리 사이에 그려진 가상의 길인 ‘황도’를 따라 매일 조금씩 이동한다(연주 운동). 그래서 이 일곱 천체는 떠돌이별, 즉 ‘행성’이라는 이름을 얻게 되었다. 달은 황도상의 한 별자리에서 시작해 한 바퀴를 돌아 동일한 별자리로 돌아오는 데 약 27.3일이 걸리고, 태양은 1년이 걸리며, 수성과 금성 역시 평균 1년이 걸린다. 그리고 화성, 목성, 토성의 평균 황도 주기(sidereal period)는 각각 687일, 12년, 30년이다. 고대인들은 황도 주기가 짧은 행성일수록 지구에 가깝다고 가정하여, 달, 수성-금성-태양, 화성, 목성, 토성의 순으로 행성들의 순서를 결정했다. 수성-금성-태양의 순서에 대해서는 다양한 견해가 있었으나, 가장 표준적인 견해는 프톨레마이오스가 제안했던 수성, 금성, 태양의 순서였다(쿤 2016, 94-100쪽).

그림 2. 외행성의 겉보기 역행 운동

달과 태양은 황도를 따라 항상 서쪽에서 동쪽으로만 ‘순행’하였다. 반면 수성, 금성, 화성, 목성, 토성은 대부분의 기간 동안 황도를 따라 서쪽에서 동쪽으로 ‘순행’하지만, 때로는 방향을 바꾸어 동쪽에서 서쪽으로 움직이는 ‘역행 운동’을 했다(그림 2). 역행 운동은 대략 일정한 간격으로 반복되는데, 수성은 대략 116일, 금성은 584일마다 역행하며, 화성, 목성, 토성은 각각 780일, 399일, 378일마다 역행 운동을 했다. 또한 이 다섯 행성은 역행 운동을 할 때마다 가장 밝아졌는데, 화성과 금성은 그 밝기 변화가 특히 심했다.

역행 운동을 하는 다섯 행성은 태양과의 관계에 따라 ‘내행성’(inferior planets)과 ‘외행성’(superior planets)으로 구분되었다. 소위 ‘내행성’으로 불린 수성과 금성은 절대로 태양으로부터 멀리 떨어지는 법이 없었다. 즉 두 행성은 해가 뜨기 직전 동쪽 하늘 또는 해가 진 직후 서쪽 하늘에서만 볼 수 있다. 이 행성들이 태양으로부터 벌어질 수 있는 최대의 각도를 ‘최대 이각’이라고 불렀는데, 수성의 최대 이각은 28°였고, 금성의 최대 이각은 45°였다. 그 결과 내행성들은 태양 앞뒤의 최대 이각 사이를 왕복하는 셔틀처럼 운동했는데, 내행성의 역행 운동은 행성이 태양과 만나는 두 종류의 ‘합’ 중에서 지구와 가까워 보이는(즉, 행성이 밝아지는) ‘내합’의 위치에서만 일어났다.

소위 ‘외행성’으로 불린 화성, 목성, 토성은 태양과의 거리에 제한이 없었다. 즉 외행성들은 태양 부근뿐만 아니라 태양 정반대편에도 있을 수 있었다. 그럼에도 그들의 운동 역시 태양과 연결되어 있었다. 외행성들은 오직 태양 반대쪽인 ‘충’의 위치에 있을 때에만 역행을 했다. 즉 역행 중인 외행성은 해가 질 무렵 그 정반대편인 동쪽에서 떠서 밤 12시에 (북반구 중위도 지역에서 관찰할 때) 남중한 후 다음날 해가 뜰 무렵 그 정반대편인 서쪽에서 진다. 반대로 외행성이 가장 빠른 속도로 순행 중일 때에는 언제나 태양과 같은 방향인 ‘합’의 위치에 있다.

그림 3. 지구 중심의 주원-주전원 체계. 주전원이 주원보다 더 빨리 돌기 때문에, 행성이 주원 안쪽을 도는 1번 위치 부근, 2번 위치 부근에서 역행이 일어나게 된다. 주원의 회전 속도는 1/T_d이고, 주전원의 회전 속도는 1/T_e이며, 1번 역행 위치에서 2번 역행 위치까지 이동하는 데 걸리는 시간은 역행 주기인 T_r과 같다. 그 시간 동안 주원은 T_r/T_d 바퀴를 도는 반면, 더 빨리 도는 주전원은 T_r/T_e 바퀴를 돈다. 이때 주전원은 주원보다 1바퀴를 더 돌아야 2번 위치에 오게 된다.

고대의 천문학자들은 항성 천구를 통해 별의 운동을 설명했듯이, 행성 천구들을 도입하여 행성의 운동을 설명하고자 했다. 다만 행성의 운동은 별보다 복잡했기에 행성마다 여러 개의 천구가 도입되었는데, 그중 가장 성공적인 것은 주원-주전원 체계였다(그림 3). 이 체계는 지구를 중심으로 균일하게 회전하는 원인 주원(周圓, deferent)과 그 원주 위의 한 점을 중심으로 균일하게 회전하는 또 다른 작은 원인 주전원(周轉圓, epicycle)으로 이루어져 있으며, 행성은 주전원의 원주 위에 있었다. 주전원은 주원과 같은 방향으로 회전하지만 그보다 빠른 속도로 회전하는 것을 가정되었다. 따라서 주전원이 주원의 바깥쪽을 돌 때는 주원과 주전원의 회전 속도가 합해져 평균보다 빨리 회전하게 되고, 주원의 가장 안쪽을 도는 도중에는 주전원의 회전이 주원의 회전을 상쇄함으로써 역행 운동을 보이게 된다. 또한 이러한 체계는 행성이 역행 운동을 할 때마다 지구와 가까워진다는 점을 통해 행성의 주기적인 밝기 변화도 설명할 수 있었다.

헬레니즘 시대 알렉산드리아 지방에서 활동한 천문학자 프톨레마이오스(AD 83?-168?)는 각 행성들에 대한 관측 결과를 이용하여 각 행성들의 주원과 주전원의 회전 주기와 두 원의 크기 비율을 결정했는데, 이렇게 완성된 체계가 바로 프톨레마이오스 체계이다. 이 체계에서 주원의 주기(T_d)는 각 행성의 황도 주기(T_s)로 간단히 결정되었으며, 주전원의 회전이 주원의 회전을 한 바퀴 따라잡을 때마다 행성의 역행 운동이 일어난다는 점을 이용하면, 주전원의 주기(T_e)는 황도 주기(T_s) 및 역행 주기(T_r)와 아래와 같은 관계를 만족해야 했다(그림 3과 그 캡션을 참고할 것).

$T_{d}=T_{s}$

$T_{e}={\frac {T_{s}\times T_{r}}{T_{s}+T_{r}}}\left(\because {\frac {T_{r}}{T_{e}}}={\frac {T_{r}}{T_{d}}}+1={\frac {T_{r}}{T_{s}}}+1\right)$

그림 4. 프톨레마이오스 체계에서 행성과 태양 사이의 관계. (a) 내행성과 태양 사이의 관계. 내행성의 주원은 태양과 동일한 주기로 운동한다. 그래서 내행성 P의 주전원의 중심 C는 항상 지구와 태양을 잇는 선분 ES 위에 위치한다. 이러한 설정은 내행성이 태양과 최대 이각 이내에서만 발견되는 이유를 설명해준다. (b) 외행성과 태양 사이의 관계. 외행성의 주전원은 태양과 동일한 주기로 운동한다. 그래서 주전원의 중심과 외행성을 잇는 선분 CP는 언제나 지구와 지구를 잇는 선분 ES와 평행을 유지하며 돈다. 이러한 설정은 외행성이 역행을 할 때마다 행성이 태양 정반대편인 ‘충’의 위치에 있는 이유를 설명해준다. (그림은 Martens 2000에서 가져옴.)

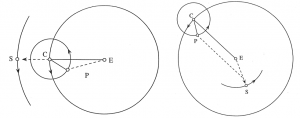
행성들에 대한 실제 관측 결과와 위의 관계식을 이용한 주전원의 주기에 대한 계산 결과는 표 1에 나타나 있다. 표 1은 앞서 언급했던 행성과 태양 사이의 관계를 보다 명시적으로 보여주고 있는데, 내행성은 그 주원의 주기가 태양의 황도 주기와 같은 1년이며, 외행성은 그 주전원의 주기가 태양의 황도 주기와 같은 1년이다. 그리고 이러한 관계는 그림 4를 통해 더욱 명확하게 드러난다. 우선 내행성인 수성과 금성의 주원은 태양과 동기화된 운동을 한다(그림 4a). 즉 태양과 동기화된 주원은 주전원의 중심 C를 항상 지구와 태양을 잇는 선분 ES 위에 위치하도록 유지시켜주며, 주전원의 회전은 행성을 태양 앞뒤로 왕복하도록 만든다. 수성과 금성의 최대 이각 차이는 주원에 대한 주전원의 크기 비율 차이로 설명되는데, 수성은 금성에 비해 상대적으로 작은 주전원/주원 비율을 가지기 때문에 작은 최대 이각을 가진다. 한편 외행성인 화성, 목성, 토성은 그 주전원이 태양과 동기화된 운동을 한다(그림 4b). 즉 주전원의 중심으로부터 행성을 잇는 선분 CP는 항상 지구와 태양을 잇는 선분 ES와 평행을 유지하며 회전함에 따라, 행성이 주원의 가장 안쪽을 도는 순간 그 행성은 역행을 하는 동시에 태양 정반대편인 ‘충’의 위치에 있게 된다. 이로써 외행성이 역행을 할 때마다 태양 정반대편에 위치하는 이유가 설명된다.

표 1. 지구 중심 체계에서의 행성의 주기.

	관측 주기		프톨레마이오스 체계
	황도 주기(Ts)	역행 주기(Tr)	주원의 주기(Td)	주전원의 주기(Te)
수성	1년	116일	1년	88일
금성	1년	584일	1년	225일
태양	1년	-	1년	-
화성	687일	780일	687일	1년
목성	12년	399일	12년	1년
토성	30년	378일	30년	1년

그림 5. 프톨레마이오스 체계의 이심(C)과 대심(Q). 주원 위의 점 F는 이심 C를 중심으로 하는 주원을 돌지만, Q를 기준으로 한 각속도가 일정하게 유지됨에 따라 A에서 가장 느려지고 B에서 가장 빨라지는 부등속 운동을 하게 된다.

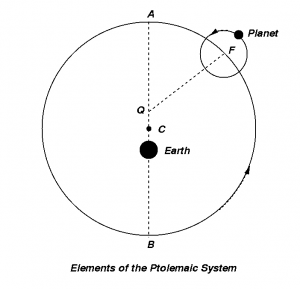
이렇게 구성된 프톨레마이오스 체계는 행성마다 주원-주전원의 크기와 회전 주기를 조정함으로써 각 행성 운동의 정성적인 특징들을 완벽하게 설명할 수 있었다. 그러나 이러한 주원-주전원 체계만을 이용한 행성 위치 예측은 여전히 상당한 오차가 있었으며, 프톨레마이오스는 이러한 오차를 없애기 위해 미세 주전원과 이심원(eccentric), 대심(equant) 등의 미세 조정 도구도 사용하였다. 이러한 도구들을 추가적으로 사용함으로써, 이제 주원의 중심은 지구(E)에서 살짝 벗어난 이심(C)이 되었고, 주원은 대심(Q)을 기준으로 동일한 각속도로 회전함에 따라 ‘부등속’ 원운동을 하게 되었다(그림 5). 그 결과 천체들의 운동은 지구를 중심으로 한 균일한 원운동의 이상을 완벽하게 지킬 수 없게 되었지만, 이러한 도구들 덕분에 프톨레마이오스의 체계는 “모든 천체 운동에 대한 완전하고, 상세하고, 정량적인 설명을 제공”(쿤 2016, 133쪽)할 수 있었고, 이러한 성취 덕분에 프톨레마이오스 체계는 이후 약 1500년 동안 서구 세계에서 표준적인 우주 체계로 자리 잡게 되었다.

코페르니쿠스 체계의 조화

코페르니쿠스(Nicolaus Copernicus)는 1543년 출판한 『천구의 회전에 관하여』의 서문에서 프톨레마이오스 체계에 대한 자신의 불만을 다음과 같이 토로했다.

이심원 체계를 고안했던 이들[프톨레마이오스 등]은 그들의 가정에 부합하는 계산을 통해 겉보기 운동을 거의 완벽하게 만들어 낸 것처럼 보이지만, 운동의 균일성이라는 제1원리를 위반하는 것처럼 보이는 많은 것들도 동시에 허용했습니다.(Copernicus 1992, Preface)

여기서 코페르니쿠스는 프톨레마이오스 체계의 정량적 성취를 인정하면서도, 그러한 성취를 위해 “운동의 균일성이라는 제1원리를 위반”하는 대가를 치렀음을 지적하고 있다. 여러 역사가들은 여기서 코페르니쿠스가 프톨레마이오스의 ‘대심’을 비판하고 있다고 해석했다(쿤 2016, 129-132쪽). 실제로 코페르니쿠스는 부등속 원운동을 만들어내는 대심의 효과를 등속 원운동을 하는 미세 주전원으로 대체하는 아랍 천문학의 기법을 도입했는데(Swerdlow 2004, 86쪽, 111-115쪽), 이를 통해 우리는 그가 행성의 운동에서 ‘운동의 균일성이라는 제1원리’를 복원시키고자 했음을 알 수 있다. 그러나 ‘대심’에 대한 코페르니쿠스의 불만이 프톨레마이오스 체계에 대한 비판적 탐구를 시작한 동기 중 하나일 수는 있지만, 태양과 지구의 자리를 맞바꾼 이유가 되긴 어렵다. 코페르니쿠스가 태양 중심 체계를 제안한 이유를 이해하기 위해서는 앞의 구절에 바로 이어진 다음의 구절도 살펴볼 필요가 있다.

또한 그것 때문에 그들은 우주의 형태나 그 부분들의 불변의 대칭성과 같은 중요한 사항은 이해하거나 도출할 수도 없게 되었습니다. 이는 마치 한 화가가 각각 다른 모델로부터 각각 아주 잘 그려진 손, 발, 머리 등을 모아 자신의 그림을 완성하나 그것이 한 사람의 모습으로는 보이지 않는 것과 같으며, 여기서 그 조각들은 서로 전혀 어울리지 않기 때문에 그 결과물은 한 명의 사람이라기보다는 괴물이 될 것입니다. (Copernicus 1992, Preface)

여기서 코페르니쿠스는 지구 중심 체계에서는 “우주의 형태나 그 부분들의 불변의 대칭성”을 이해하거나 도출할 수 없다고 말한다. 코페르니쿠스는 이를 미적으로 부조화스러운 그림에 빗대고 있는데, 그는 지구 중심 체계의 각 부분들이 “서로 전혀 어울리지 않아 그 결과물은 한 명의 사람이라기보다는 괴물”과 같다고 말한다. 그러면서 그는 태양과 지구의 자리를 맞바꾼 태양 중심 체계의 장점을 다음과 같이 대비시킨다.

지구에 부여한 운동들을 가정하고서 오랫동안 많은 관측을 한 결과, 다른 행성들의 운동을 지구의 회전과 관련지은 후 각 행성의 공전에 맞춰 계산해 본다면 행성들의 모든 현상이 그로부터 곧장 따라 나온다는 것을 발견하게 되었습니다. 뿐만 아니라 모든 행성들과 천구들, 또는 하늘 그 자체의 순서와 크기가 서로 너무도 밀접하게 묶여 있어서, 그것의 어떤 부분도 다른 모든 부분과 우주 전체를 교란하지 않고선 변경될 수 없다는 것도 발견했습니다.(Copernicus 1992, Preface)

이러한 코페르니쿠스의 말에 따르면, 태양 중심 체계는 첫째, 지구의 회전을 고려함으로써 “행성들의 모든 현상이 그로부터 곧장 따라 나온다”는 장점이 있으며, 둘째, “그것의 어떤 부분도 다른 모든 부분과 우주 전체를 교란하지 않고선 변경될 수 없다”는 장점이 있다. 이러한 태양 중심 체계의 장점은 『천구의 회전에 관하여』 1권 10장에서 다음과 같이 상술된다.

지구를 우주의 중심에 놓게 되면 수많은 천구가 필요해져 문제를 혼란스럽게 만들 수밖에 없는데, 그보다는 이것[태양중심설]을 믿는 것이 더 낫다고 생각한다. 우리는 쓸모없거나 불필요한 것들을 하나도 만들어 내지 않으면서 여러 작용에 하나의 원인을 부여하길 좋아하는 자연의 지혜를 따르는 것이 낫다. … 우리는 이러한 천체들의 배열 아래 놓여 있는 우주[태양 중심의 우주]의 놀라운 대칭성과 다른 방식으로는 결코 발견할 수 없는 천구의 운동과 크기 사이의 조화로운 관계를 발견하게 된다.(Copernicus 1992, 1권 10장))

이 인용문의 앞부분에서 코페르니쿠스는 “지구를 우주의 중심에 놓게 되면 수많은 천구가 필요해져 문제를 혼란스럽게 만들 수밖에 없는” 반면에, 태양 중심 체계에서는 그러한 “쓸모없거나 불필요한 것들을 하나도 만들어 내지 않으면서 여러 작용에 하나의 원인을 부여”할 수 있다고 말한다. 그리고는 태양 중심의 우주에서는 “우주의 놀라운 대칭성과 다른 방식으로는 결코 발견할 수 없는 천구의 운동과 크기 사이의 조화로운 관계”를 발견할 수 있다고 역설한다. 그렇다면 이러한 코페르니쿠스의 논변들은 어떻게 해석되어야 할까? 가장 통속적인 해석은 태양 중심 체계가 지구 중심 체계에서 사용하던 수많은 주전원을 제거함으로써 우주 체계의 단순성을 회복했다는 것이다. 이러한 해석은 쿤이 『코페르니쿠스 혁명』에서 썼던 다음의 구절과 결합하여 널리 유포되었다.

프톨레마이오스 자신이 『알마게스트』에서 구현했던 것 말고도 수많은 버전의 프톨레마이오스 체계가 있었고, 그들 중 일부는 행성의 위치를 예측하는 데 상당한 정확성을 달성했다. 그러나 그 정확성은 예외 없이 복잡성−새로운 미세 주전원이나 그와 동등한 장치의 추가−을 대가로 내주고서 얻은 것이었고, 증가한 복잡성은 행성 운동에 대한 최종 결과가 아닌 고작 더 나은 근사치를 제공했을 뿐이었다. 이 체계의 어떤 버전도 정밀해진 후속 관찰에 의한 시험을 제대로 견뎌 낸 적이 없었고, 이러한 실패는, 더 투박한 버전의 2구체 우주를 그토록 신빙성 있어 보이게 해 주었던 개념적 경제성이 완전히 소멸하는 것과 결합해, 종국에 코페르니쿠스 혁명으로 이어졌다.(쿤 2016, 2장 6절)

그러나 깅거리치(Gigerich 1993)와 스워들로우(Swerdlow 2004, 85쪽)를 비롯한 여러 학자들은 프톨레마이오스 이래 주전원의 증가가 거의 없었다는 점을 보인 바 있다. 또한 쿤 본인도 코페르니쿠스의 체계가 역행 운동 등의 설명을 위해 도입된 기본 주전원을 없앴을 뿐 여전히 수많은 미세 주전원들을 사용했다는 점을 인정하고 있다. 따라서 원의 개수에만 초점을 맞춘 위의 해석은 설득력이 부족하다. 이러한 문제로 인해 대칭성과 조화에 의거한 코페르니쿠스의 논변은 그와는 다른 방식으로 이해될 필요가 있다. 여기서 나는 코페르니쿠스의 논변을 세 가지로 구분하여 이해하고자 한다. 첫 번째는 우주 구조의 확정에 의거한 논변, 두 번째는 행성의 공전 주기와 궤도 사이의 조화에 의거한 논변, 세 번째는 현상들 사이의 상호연관성(interconnectedness)에 의거한 논변이다.

우주 구조의 확정

“지구를 우주의 중심에 놓게 되면 수많은 천구가 필요해져 문제를 혼란스럽게 만들 수밖에 없”다는 코페르니쿠스의 언급은 행성들의 순서에 대해 논의하던 중에 나온 것이었다. 그 구절 바로 앞부분에서 그는 지구를 중심에 놓았던 과거의 학자들이 수성과 금성과 태양의 순서에 대해 확정하지 못했음을 지적하고 있었다. 기본적으로 지구 중심의 우주 체계에서 관측을 통해 도출할 수 있는 크기는 각 행성의 주전원/주원의 크기 비율뿐이었다. 원한다면 그들은 관측에 아무런 변화를 주지 않으면서도 주전원과 주원의 크기를 둘의 비율만 유지한 채 마음대로 늘렸다 줄였다 할 수 있었다. 이러한 점에 주목한 마르텐스(Martens 2008, 263-264쪽)는 코페르니쿠스의 “수많은 천구가 필요”하다는 언급이 지구 중심의 체계의 복잡성이 아닌 그것의 불확정성과 지나친 유연성을 비판하고 있는 것이라고 주장했다. 즉 지구 중심의 체계에서는 행성 천구의 크기들을 확정할 수 없으며, 따라서 행성들의 순서에 대한 논란도 해결할 수 없다는 것이다.

그림 6. 태양 중심 체계에서 궤도의 상대 크기 계산하기. (a) 내행성의 경우. 이각 SEP가 최댓값에 도달할 때 각 SPE는 직각이 되어야 한다. 행성(P), 태양(S), 지구(E)는 하나의 직각삼각형을 형성하며, 그 예각 SEP는 직접 측정될 수 있다. 그런데 직각삼각형의 한 예각을 알면 그 삼각형의 변의 길이비들이 결정된다. 따라서 지구의 궤도 반지름 SE 대 내행성의 궤도 반지름 SP의 비는 각 SEP의 측정값으로부터 계산될 수 있다. (b) 외행성의 경우. 어떤 알려진 순간에 태양, 지구, 행성 모두가 직선 SEP상에 놓여 있다고 가정해 보자. 이는 그 행성이 황도상에서 태양과 정반대 방향에 있을 때이며, 역행 운동을 하고 있는 중이다. 지구는 자기 궤도를 어떤 외행성보다도 빨리 돌기 때문에, 얼마 후에 지구 E'와 행성 P'가 태양과 직각삼각형 SE'P'를 형성하는 순간이 오기 마련이고, 각 SE'P'는 지구에서 바라보는 태양과 그 외행성 사이의 각이기 때문에, 그것은 직접 결정될 수 있고 그 지점에 도달하는 데 걸리는 시간도 측정될 수 있다. 이제 각 ESE'가 계산될 수 있는데, 360° 대 그 값의 비는 지구가 자기 궤도를 한 바퀴 도는 데 걸리는 365일 대 지구가 E에서 E'로 움직이는 데 걸리는 시간의 비와 같아야 하기 때문이다. 각 PSP'는 정확히 똑같은 방식으로 결정될 수 있는데, 그 행성이 자기 궤도를 한 바퀴 도는 데 걸리는 시간은 이미 알고 있고, 그 행성이 P에서 P'까지 가는 데 걸리는 시간은 지구가 E에서 E'까지 가는 데 걸리는 시간과 같기 때문이다. 그러면 우리는 또 다시 한 예각 P'SE'를 알고 있는 직각삼각형 SE'P'를 얻게 되고, 따라서 지구 궤도 반지름 SE' 대 행성 궤도 반지름 SP'의 비는 내행성 때와 똑같이 결정될 수 있다.

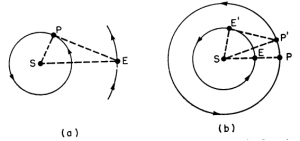
반면에 코페르니쿠스의 체계는 태양을 중심으로 한 지구의 운동을 가정함으로써 행성 천구의 크기를 직접 확정할 수 있었다. 코페르니쿠스의 체계에서 태양 앞뒤를 왕복할 뿐인 수성과 금성은 단지 지구보다 안쪽 궤도를 가진 것으로 이해되었고, 그것만으로 그들의 겉보기 운동은 완벽히 설명됨과 동시에 각 내행성의 공전 궤도 반경은 직각삼각형의 원리에 의해 간단하게 결정됐다. 즉 태양 중심의 체계에서, 지구의 공전 궤도 반경을 1로 둘 때, 28°의 최대 이각을 가진 수성은 0.4(≒sin28°), 45°의 최대 이각을 가진 금성은 0.7(≒sin45°)의 공전 궤도 반경을 가진 것으로 결정된다(그림 6a). 화성, 목성, 토성은 내행성보다는 다소 복잡한 계산이 필요하지만(그림 6b), 그들의 궤도 반경 역시 각각 1.5, 5.2, 9.5의 값으로 계산 가능했다(표 2). 즉 코페르니쿠스가 “수많은 천구”를 통해 지구 중심 체계와 대비하고자 했던 태양 중심 체계의 장점은 행성 천구(궤도)들의 순서와 크기를 확정할 수 있다는 것으로 해석 가능하다.

이러한 해석은 코페르니쿠스가 사용한 “불변의 대칭성”이란 말의 어색함도 없애준다. 사실 오늘날 사용하는 “대칭성(symmetry)”의 표준적인 의미에 비추어볼 때, 코페르니쿠스 체계는 전혀 대칭적이지 않다. 그 체계는 선대칭도 점대칭도 보여주지 않는다. 또한 현대 물리학의 용법인 “특정한 변환에도 변치 않음”과도 잘 어울리지 않는다. 혼과 골드슈타인(Hon and Goldstein 2004)은 코페르니쿠스가 사용한 “대칭성”이 “적절한 비율”이라는 의미였음을 주장한다. 그들에 따르면, 비트루비우스 등의 고대 그리스의 학자들은 “대칭성”을 그림이나 조각, 건축물과 같은 대상에 대해 “그것의 여러 부분들이 서로 적합한 비율로 구성되어 있음”이란 의미로 사용했는데, 코페르니쿠스는 그 의미의 “대칭성”을 자신의 태양 중심의 우주 체계에 적용함으로써 각 행성 천구들의 크기가 적합한 비율로 구성되어 있다는 점을 강조했다는 것이다. 또한 코페르니쿠스는 그 비율이 지구를 포함한 모든 행성들이 태양을 중심으로 돈다는 가정과 몇 가지 관찰을 통해 각각 하나의 값으로 확정된다는 점(표 2)에 주목함으로써 지구 중심 체계에서는 “우주의 형태나 그 부분들의 불변의 대칭성”을 도출할 수 없다고 비판함과 동시에, 태양 중심 체계에서는 “우주의 놀라운 대칭성”을 발견할 수 있다고 말할 수 있었던 것이다.

‘대칭성’과 ‘조화’에 대한 이러한 코페르니쿠스의 관점은 당대의 미술 이론과도 상당한 연관이 있다. 과학사가 웨스트만(Westman 1975)은 ‘조화’에 대한 코페르니쿠스의 관점이 당시 르네상스 시대에 예술과 건축 등 전 분야에 걸쳐 널리 퍼져 있던 균형과 조화에 대한 관점과 같음을 지적했고, 토퍼(Topper 2007, 34쪽)는 당대 이탈리아의 예술가 알베르티(Leon Battista Alberti, 1404-1472)나 바사리(Giorgio Vasari, 1511-1574)가 ‘아름다움’에 대해 언급한 구절들을 인용함으로써, 코페르니쿠스가 그와 유사한 미적 관점을 과학 이론에 적용했음을 지적했다. 예컨대 알베르티는 1452년 출판한 그의 『건축론(Ten Books on Architecture』에서 “나는 아름다움을 모든 부분들의 조화로서, … 어떠한 추가나 삭제나 변경도 전보다 나빠지게 만들 뿐인 그러한 비율과 연결로 함께 결합되어 있는 상태로서 정의할 것이다”(Alberti 1955, 113쪽)라고 말하고 있다. 이러한 관점을 인물화에 적용할 때, 인물화가 아름답기 위해서는 몸을 구성하는 각 부분들이 적절한 비율로 함께 잘 결합되어 있어야 했다. 만약 코페르니쿠스가 이러한 아름다움에 대한 당대의 전체론적 관점을 공유하고 있었다면, 각 행성들의 운동이 개별적으로만 모형화될 수 있을 뿐 함께 적절한 비율로 결합될 수 없었던 지구 중심 체계는 그에게 “마치 한 화가가 각각 다른 모델로부터 각각 아주 잘 그려진 손, 발, 머리 등을 모아 자신의 그림을 완성하나 그것이 한 사람의 모습으로는 보이지 않는 것과 같으며, 여기서 그 조각들은 서로 전혀 어울리지 않기 때문에 그 결과물은 한 명의 사람이라기보다는 괴물”처럼 보였을 것이다.

행성의 공전 주기와 궤도 반경 사이의 조화

표 2. 태양 중심 체계에서 발견되는 행성들의 공전 주기와 궤도 반경 사이의 조화로운 관계.

	공전 주기	궤도 반경
수성	88일	0.4
금성	225일	0.72
지구	1년	1
화성	687일	1
목성	12년	5.2
토성	30년	9.5

두 번째 의미의 조화는 첫 번째의 의미의 조화의 연장선상에서 해석될 수 있다. 코페르니쿠스는 태양 중심 체계에서는 “우주의 놀라운 대칭성”뿐 아니라 “천구의 운동과 크기 사이의 조화로운 관계”도 발견할 수 있다고 주장했다. 이 조화로운 관계는 “천구의 운동과 크기 사이”의 관계로 매우 명시적으로 제한되어 있기 때문에, 웨스트만(Westman 1975)이나 골드슈타인(Goldstein 2002) 등의 역사학자들은 이를 쉽게 해석할 수 있었다. 즉 여기서의 조화로운 관계는 천구의 회전 주기가 증가할수록 천구의 크기도 함께 증가하는 ‘단조 증가’의 관계를 의미한다.

지구의 운동을 가정함으로써 확정된 각 행성의 공전 궤도 반경은 이제 각 행성의 공전 주기와 비교될 수 있는데, 이는 표 2에 그려져 있다. 이에 따르면, 태양과 지구의 자리를 맞바꾼 태양 중심 체계에서 지구의 공전 주기는 표 1에 표시된 태양의 황도 주기와 같고, 수성과 금성의 공전 주기는 표 1에 표시된 각 행성의 주전원의 주기와 같으며(그 이유는 그림 5c에서 설명됨), 나머지 행성들의 공전 주기는 표 1에 표시된 각 행성의 황도 주기와 같다. 표 1과 비교할 때, 태양 중심 체계에서는 행성마다 하나의 공전 주기와 하나의 궤도 반경이 결정되며, 그 공전 주기가 증가할수록 궤도 반경도 증가한다.

사실 지구 중심 체계에서도 행성들의 순서는 행성의 황도 주기가 증가할수록 더 큰 천구를 가질 것이라는 오래된 직관에 의해 의존하여 결정됐다. 그러나 행성들의 순서가 그 황도 주기에 의해 결정될 것이라는 직관은 일부 행성들에 적용될 수 없었다. 즉 수성, 금성, 태양은 동일한 황도 주기를 가지고 있었기에, 그 주기만으로는 그들의 순서를 확정할 수 없었으며, 따라서 이러한 지구 중심 체계에서는 행성들의 순서를 어떻게 결정하든, 그 우주 체계는 황도 주기는 같지만 궤도 반경은 다른 행성들을 포함할 수밖에 없다. 반면에 코페르니쿠스의 태양 중심 체계에서는 행성 천구의 회전 주기가 증가할수록 그 천구의 크기도 함께 증가한다. 바로 이러한 점 때문에 코페르니쿠스는 태양 중심 체계에서는 “다른 방식으로는 발견할 수 없는 천구의 운동과 크기 사이의 조화로운 관계를 발견할 수 있다”고 말한 것이다. 후에 케플러는 둘 사이의 정량적인 관계식, 즉 공전 주기의 제곱이 궤도 반경의 세제곱에 비례한다는 케플러 제3법칙을 발견한 후 그에 “조화의 법칙”이라는 이름을 붙여 주었는데, 이는 코페르니쿠스의 의도에 정확히 부합하는 이름이었을 것이다.

상호연관성

세 번째 의미의 조화인 ‘상호연관성’은 태양과 지구의 자리를 맞바꾸어 태양을 중심으로 도는 지구의 운동을 가정하면 지구 중심 체계에서는 무관했던 수많은 현상들이 상호연관된 현상들로 이해될 수 있다는 것이다. 지구 중심 체계에 비해 태양 중심 체계가 가진 상호연관성을 가장 명확하게 보여줄 수 있는 부분은 행성의 운동과 태양의 겉보기 운동에서 나타나는 모종의 관계이다. 앞서 언급했듯이 고대인들은 행성의 운동이 태양과 특정한 방식으로 관련되어 있다는 것을 알고 있었으며, 프톨레마이오스는 이를 설명하기 위해 내행성의 주원과 외행성의 주전원이 태양과 동기화되어 움직이는 우주 체계를 완성했다(그림 4, 표 1). 그러나 원래의 지구 중심의 주원-주전원 체계에서 각 행성은 독립적인 주원-주전원을 가지는 것이기에, 그 운동이 다른 행성인 태양의 운동과 동기화되어 있어야 할 이유는 없었다. 만약 프톨레마이오스에게 그러한 동기화의 이유를 묻는다면, 가능한 답은 ‘우연’ 또는 알 수 없는 ‘신의 의도’ 뿐일 것이다. 또한 그러한 동기화의 메커니즘을 묻더라도 그는 답을 할 수 없었을 것이다. 어떻게 별개의 원들이 한 치의 오차 없이 동일한 주기로 돌 수 있겠는가?

그림 7. 태양 중심 체계에서 태양, 지구, 외행성의 관계. 1번 역행부터 2번 역행까지의 시간(T_r) 동안 지구(E)는 행성(P)보다 한 바퀴를 더 돌게 된다.

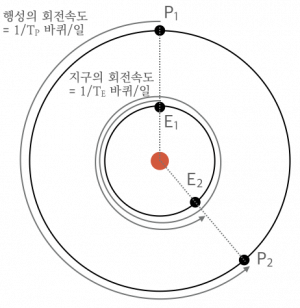
반면 코페르니쿠스의 태양 중심 체계는 지구를 포함한 각 행성들이 태양을 중심으로 돌고 있다는 점을 이론의 핵심 가설로 삼기 때문에, 지구에서 관측된 각 행성들의 겉보기 운동이 지구에서 관측된 태양의 겉보기 운동(실제로는 지구의 공전)과 관련되어 있는 것은 이론의 필연적인 귀결이 된다. 지구는 태양을 중심으로 공전하며, 그 공전 주기는 관측을 통해 결정된 태양의 황도 주기인 1년으로 결정된다. 만약 어떤 행성의 공전 궤도가 지구의 공전 궤도보다 작다면, 지구에서 보기에 그 행성은 마치 태양을 따라다니며 그 앞뒤를 특정한 주기로 왕복하는 것처럼 보일 것이며, 따라서 그 행성의 평균 황도 주기는 태양의 황도 주기와 일치해야 할 것이다. 즉 내행성의 황도 주기와 태양의 황도 주기 사이의 일치는 태양중심설의 필연적인 귀결이다(그림 6a). 한편 어떤 행성의 공전 궤도가 지구의 공전 궤도보다 크다면, 지구에서 보기에 그 행성의 공전 주기는 행성의 관측된 평균 황도 주기와 일치하지만 지구의 운동이 그 행성의 운동을 따라잡을 때마다 겉보기에 역행 운동이 나타나게 된다. 태양을 도는 지구가 외행성을 따라잡는 순간은 태양-지구-외행성이 일렬로 배치되는 순간이므로, 외행성의 역행이 태양 정반대편에서만 일어난다는 관찰은 태양 중심 체계로부터 곧바로 도출된다. 이러한 원리를 이용하면, 태양중심설은 지구의 공전 주기 T_E(즉, 태양의 황도 주기)와 외행성의 공전 주기 T_P 및 역행 주기 T_r 사이에 다음과 같은 관계가 성립해야 한다는 귀결을 가진다(그림 7).

${\frac {T_{r}}{T_{E}}}-{\frac {T_{r}}{T_{P}}}=1$

즉 지구 중심 체계에서는 서로 무관해 보였던 태양의 황도 주기와 행성의 황도 주기 및 역행 주기가 태양 중심 체계에서는 밀접하게 연결되어 있을 수밖에 없는 것으로 드러나게 된다. 따라서 그중 두 가지, 예컨대 태양의 황도 주기와 외행성의 공전 주기가 결정되면 외행성의 역행 주기가 도출되고, 이를 통해 우리는 행성들이 하필 그러한 역행 주기를 가지게 되는지 이해할 수 있게 된다.

이러한 태양 중심 체계의 상호연관성을 직관적으로 확인할 수 있는 방법이 한 가지 있다. 위의 관계식에 따르면, 외행성은 그 공전 주기 T_P가 커질수록 역행 주기 T_r이 점점 작아져 지구의 공전 주기인 1년에 점점 근접해야 한다는 사실이 도출된다. 정말로 화성보다 훨씬 느리게 도는 목성의 역행 주기는 399일로 화성의 역행 주기 780일보다 작고, 목성보다 느리게 도는 토성의 역행 주기는 378일로 목성의 역행 주기보다 작으며 그 값이 거의 1년에 근접하고 있는데, 이는 태양 중심 체계에서는 그들의 궤도 순서에 의해 당연히 그래야만 하는 현상으로 이해될 수 있다. 반면 지구 중심 체계에서는 지구의 주기(관측상으로는 태양의 주기)와 다른 행성들의 주기 사이에 그러한 관계가 성립해야 할 필연적인 이유가 존재하지 않는다. 바로 이러한 이유 때문에 코페르니쿠스는 다음과 같이 얘기할 수 있었던 것이다.

왜냐하면 이[태양 중심의 배치] 덕분에 우리는 왜 목성의 순행과 역행은 토성보다는 크고 화성보다는 작게 보이는지, 어째서 금성의 순행과 역행이 수성보다 크게 보이는지, 어째서 이런 방향 전환이 목성보다 토성에서 더 자주 일어나지만 수성에 비해 화성과 금성에서는 덜 자주 일어나는지, 또한 어째서 토성, 목성, 화성이 태양에 가려지거나 낮에 뜰 때보다 태양 반대편에 있을 때 지구에 더 가까운지 … 이해할 수 있기 때문이다. 이 모든 현상은 동일한 원인에 의해 일어나는 것들로, 그 원인은 바로 지구의 운동이다.(Copernicus 1992, 1권 10장)

행성들에 대한 관측 현상들 사이의 이러한 밀접한 상호연관성은 앞서 알베르티가 얘기했던 아름다움의 정의와도 일맥상통한다. 그에게 아름다움이란 “어떠한 추가나 삭제나 변경도 보다 나쁘게 만들 뿐인 그러한 비율과 연결로 함께 결합되어 있는 상태”이다. 만약 코페르니쿠스가 이러한 관점을 공유했다면, 코페르니쿠스는 관측에 따라 자유롭게 수정될 수 있는 지구 중심 체계보다, “모든 행성들과 천구들, 또는 하늘 그 자체의 순서와 크기가 서로 너무도 밀접하게 묶여 있어서, 그것의 어떤 부분도 다른 모든 부분과 우주 전체를 교란하지 않고선 변경될 수 없[는]”(Copernicus 1992, 서문) 태양 중심의 체계가 미적으로 더 만족스러웠을 것이다.

코페르니쿠스 체계의 조화와 증거

(이 부분은 현재 작성중. 수업을 위해 들어온 학생들은 앞부분까지만 읽을 것)

참고문헌

• Alberti, Leon Battista (1955), Ten Books on Architecture (english translation). London: A. Tiranti.
• Carman, Christián (2009), “Rounding Numbers: Ptolemy’s Calculation of the Earth–Sun Distance”, Archive for History of Exact Sciences 63, 205–242.
• Carman, Christián, and José Díez (2015), “Did Ptolemy Make Novel Predictions? Launching Ptolemaic Astronomy into the Scientific Realism Debate”, Studies in History and Philosophy of Science 52, 20-34.
• Copernicus, Nicholas (1992), On the Revolutions, translation and commentary by Edward Rosen. Johns Hopkins University Press.
• Forster, Malcolm (2004), “Simplicity and Unification in Model Selection” (manuscript), Occam’s Razor and the Relational Nature of Evidence. URL = <http://philosophy.wisc.edu/forster/520/Chapter%203.pdf>
• Gingerich, Owen (1993). The Eye of Heaven: Ptolemy, Copernicus, Kepler. New York: American Institute of Physics.
• Goldstein, B. R. (2002). “Copernicus and the Origin of His Heliocentric System”, Journal for the History of Astronomy 33, 219–235.
• Glymour, Clark (1980), Theory and Evidence. Princeton, N.J.: Princeton University Press.
• Hon, G. & B. R. Goldstein (2004), “Symmetry in Copernicus and Galileo”, Journal for the History of Astronomy 35, 273-292.
• Kuhn, Thomas S. (1996), The Structure of Scientific Revolutions, 3rd edtion. The University of Chicago Press.
• Martens, Rhonda (2000), Kepler's Philosophy and the New Astronomy. Princeton University Press.
• Martens, Rhonda (2009), “Harmony and Simplicity: Aesthetic Virtues and the Rise of Testability”, Studies in History and Philosophy of Science 40, 258-266.
• Myrvold, Wayne C. (2003), “A Bayesian Account of the Virtue of Unification”, Philosophy of Science 70, 399-423.
• Sober, Elliott (2015), Ockham's Razors: A User's Manual. Cambridge University Press.
• Swerdlow, N. M. (2004), “An Essay on Thomas Kuhn’s First Scientific Revolution, The Copernican Revolution”, Proceedings of the American Philosophical Society 148, 64-120.
• Topper, David R. (2007), “The Rationality of Simplicity: Copernicus on Planetary Motion”, Quirky Sides of Scientists: True Tales of Ingenuity and Error from Physics and Astronomy. Springer-Verlag New York, pp. 25-41.
• Westman, Richard S. (1975). “Three responses to the Copernican Theory: Johannes Praetorius, Tycho Brahe, and Michael Maestlin”, in Richard S. Westman (ed.), The Copernican Achievement, Berkeley, CA: University of California Press. pp. 285–345.
• 쿤, 토머스 (1997), 「객관성, 가치 판단, 그리고 이론 선택」, 조인래 (편역), 『쿤의 주제들: 비판과 대응』, 서울: 이화여자대학교 출판부, 299-326쪽.
• 쿤, 토머스 (2016), 『코페르니쿠스 혁명: 행성 천문학과 서구 사상의 발전』 [정동욱 옮김], 서울: 지식을만드는지식.
• 포퍼, 칼 (1994), 『과학적 발견의 논리』 [박우석 옮김], 서울: 고려원.

관련 항목

• 프톨레마이오스 체계 시뮬레이션 http://astro.unl.edu/naap/ssm/animations/ptolemaic.html
• 코페르니쿠스 체계와 프톨레마이오스 체계의 경험적 동등성 https://youtu.be/huxp4kWQnB8