프톨레마이오스 체계와 코페르니쿠스 체계 사이의 변환
정동욱, 정원호, 「위기 없는 혁명: 코페르니쿠스 혁명을 중심으로」, 『과학철학』 23권 2호, 1-51쪽 중 42-44쪽.
지구 중심의 프톨레마이오스 체계는 지구에서 관측되는 행성의 겉보기 위치에 대해 태양 중심의 코페르니쿠스 체계와 경험적으로 동등한 결과를 산출한다. 이러한 동등성은 티코 체계를 경유하는 기하학적 변환을 통해 증명되는데, 이는 아래의 그림들을 통해 설명될 수 있다.
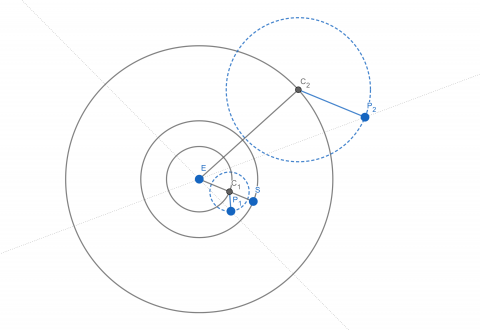
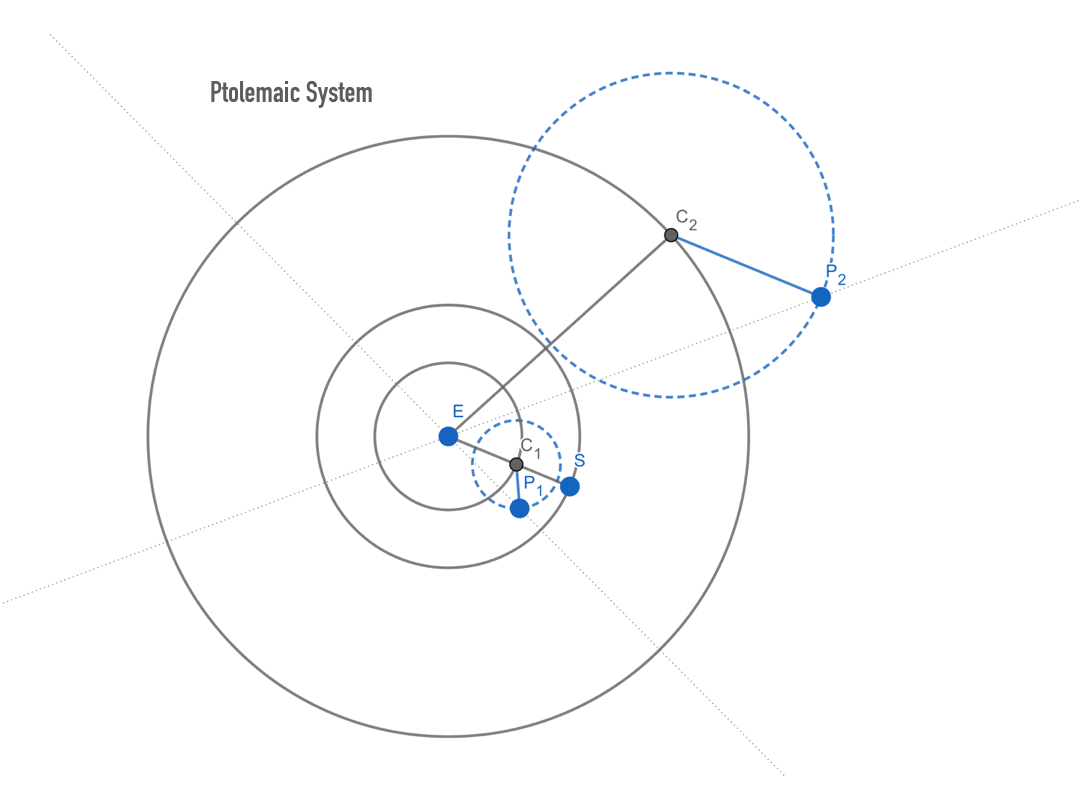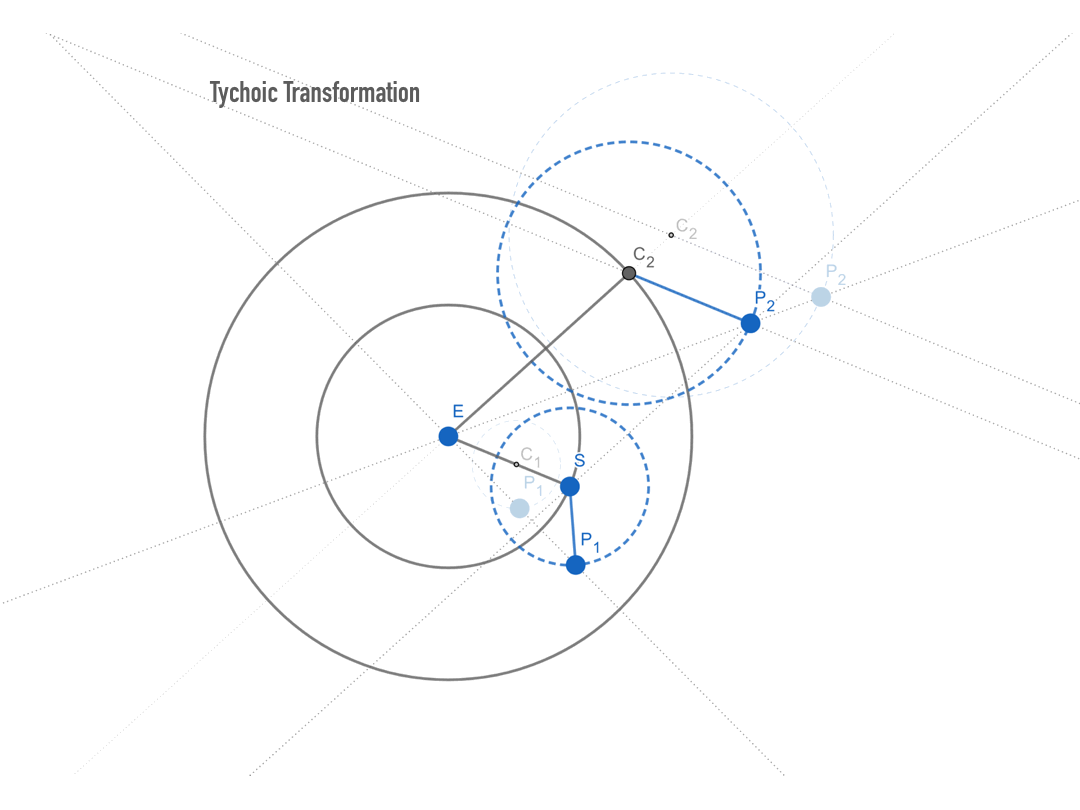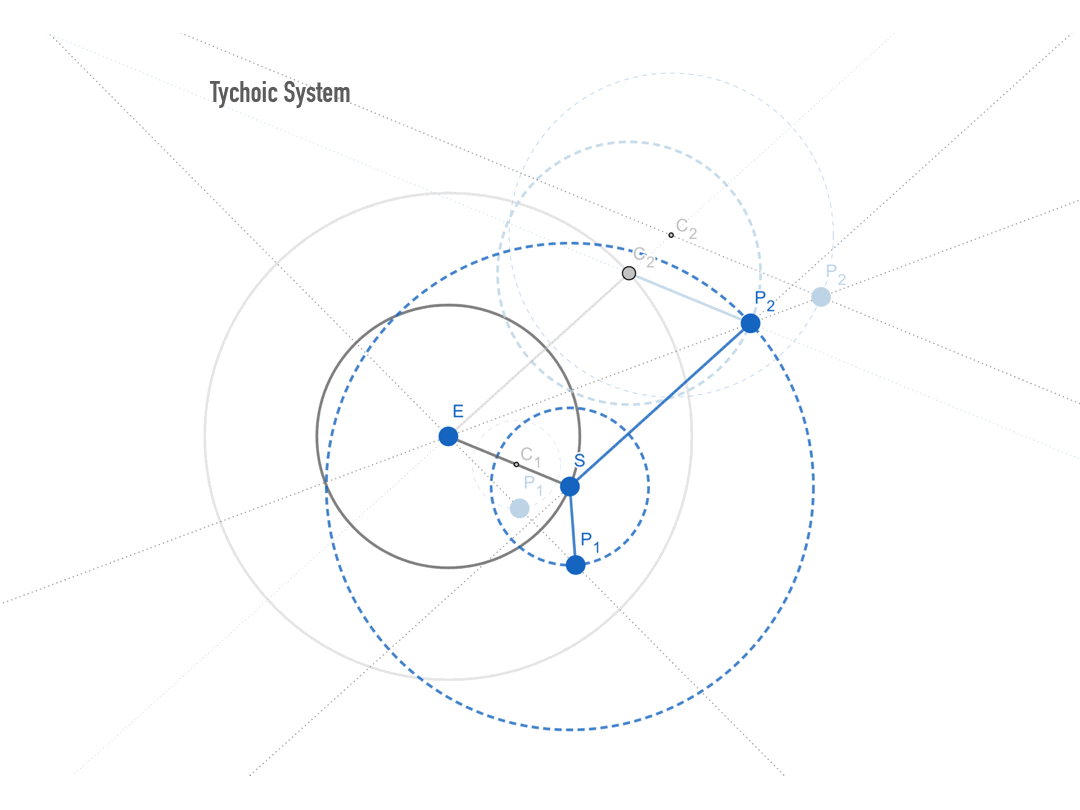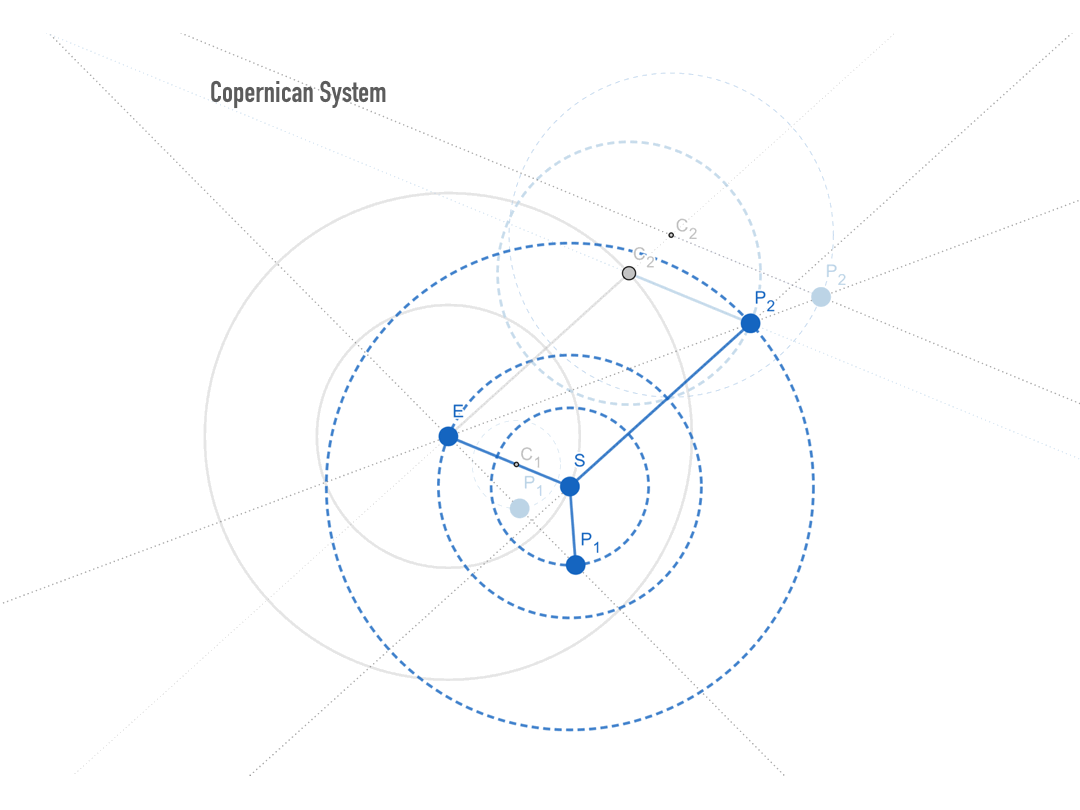
[그림 4a] 프톨레마이오스 체계
[그림 4b] 티코 체계로의 변환
그림 4a. 프톨레마이오스 체계. 프톨레마이오스 체계의 기본 형태는 지구 E를 중심으로 균일하게 회전하는 원인 주원(周圓, deferent)과 그 원주 위의 한 점을 중심으로 균일하게 회전하는 또 다른 작은 원인 주전원(周轉圓, epicycle)으로 이루어져 있으며, 행성은 주전원의 원주 위에 있다. 그런데 프톨레마이오스 체계에서 역행 운동을 하는 다섯 행성은 역행 운동을 하지 않는 행성인 태양을 기준으로 내행성과 외행성으로 구분된다. 내행성(수성, 금성)은 태양으로부터 멀리 떨어지지 못한 채 태양 앞뒤를 왕복하는 셔틀처럼 운동한다. 반면 외행성(화성, 목성, 토성)은 태양 부근뿐만 아니라 태양 정반대편에도 있을 수 있지만, 오직 태양 반대쪽인 ‘충’의 위치에 있을 때에만 역행을 한다. 이를 설명하기 위해 프톨레마이오스 체계에서 다섯 행성의 운동은 태양과 정확히 동기화되어 있다. 내행성의 경우엔 주원의 운동이 태양과 동기화된 반면, 외행성의 경우엔 주전원의 운동이 태양과 동기화되어 있다. 즉 내행성 P1의 경우 그 주전원의 중심(C1)은 항상 지구(E)와 태양(S)을 잇는 선분 ES 위에 위치하며, 외행성 P2의 경우 그 주전원의 중심(C2)과 행성(P2)을 잇는 선분 C2P2는 항상 지구(E)와 태양(S)을 잇는 선분 ES와 평행을 유지한 채 돈다.
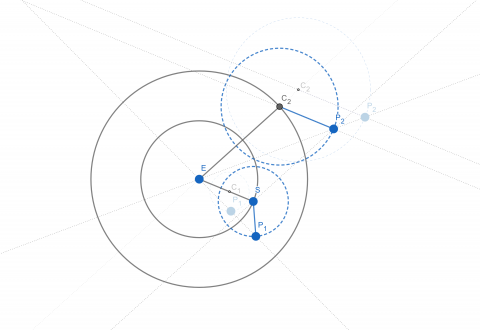
그림 4b. 티코 체계로의 변환. 프톨레마이오스 체계의 각 행성마다 주원의 반지름 R에 대한 주전원의 반지름 r의 비율 r/R을 유지한 채 그 크기를 변화시킨다. 내행성(P1)의 경우엔 C1P1/EC1의 값을 유지한 채 EC1의 길이가 ES와 같도록 확대하고, 외행성(P2)의 경우엔 C2P2/EC2의 값을 유지한 채 C2P2의 길이가 ES와 같도록 변화시킨다. 이러한 변환에도 불구하고 지구에서 관측되는 행성의 방향은 달라지지 않는다. 그림 4a와 4b에서 지구(E)에서 행성 P1과 P2를 향하는 반직선의 방향이 완벽하게 동일하다는 점에 주목하라.
[그림 4c] 티코 체계
[그림 4d] 코페르니쿠스 체계
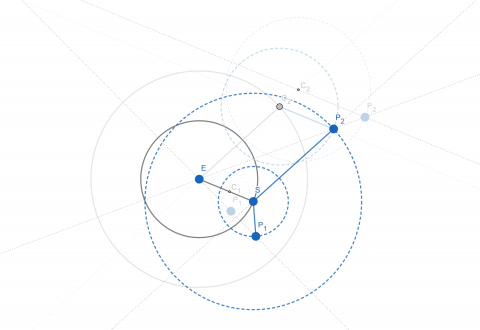
그림 4c. 티코 체계. 내행성 P1은 지구를 중심으로 도는 태양 S를 중심으로 돌게 된다. 또한 사각형 ESP2C2는 항상 평행사변형을 이루므로, 외행성 P2 역시 지구를 중심으로 도는 태양 S를 중심으로 도는 것과 다름없다. 즉 이 체계에서는 지구를 중심으로 태양이 돌고, 그러한 태양을 중심으로 나머지 행성들이 돈다.
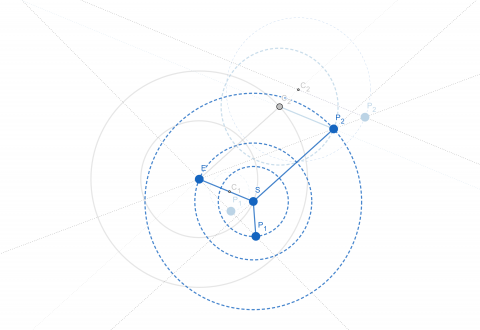
그림 4d. 코페르니쿠스 체계로의 변환. 티코 체계에서 지구(E)에 꽂혀 있던 압정을 뽑아 태양(S)에 꽂아보자. 그러면 지구마저도 태양을 중심으로 돌게 되므로, 결국 지구를 포함한 모든 행성들이 태양을 중심으로 돌게 된다. 이러한 변환에도 불구하고, 지구에서 관측되는 행성들의 방향은 여전히 그림 3a의 지구에서 관측되는 행성들의 방향과 동일하다.
단, 이러한 기하학적 동등성은 물리적 동등성을 의미하진 않는다. 기하학적 동등성에도 불구하고, 천구와 같은 행성 운동의 물리적 메커니즘을 고려할 때 코페르니쿠스는 프톨레마이오스 체계나 티코 체계보다 자신의 체계가 더 그럴듯하다고 생각했다(원 논문의 4.3절 참고).
움직이는 gif
위의 그림들을 모으면 아래와 같은 애니메이션을 만들 수 있다. 프톨레마이오스 체계에서 티코 체계를 거쳐 코페르니쿠스 체계로 변환되는 과정에서, 지구에서 바라본 행성의 방향, 즉 직선 EP1, EP2가 변하지 않는다는 점에 주목하라.
