"양자역학의 형식적 구조"의 두 판 사이의 차이
(→수학적 기초) |
|||
| 48번째 줄: | 48번째 줄: | ||
*벡터공간의 차원 : 직교벡터의 최대개수. | *벡터공간의 차원 : 직교벡터의 최대개수. | ||
*N-차원 공간의 기저(basis) : N개의 직교단위(orthonormal) 벡터들. | *N-차원 공간의 기저(basis) : N개의 직교단위(orthonormal) 벡터들. | ||
*기저를 이용한 벡터의 표현 : <math> | B \rangle = b_1 | A_1 \rangle + b_2 | A_2 \rangle + \cdots + b_N | A_N \rangle | *기저를 이용한 벡터의 표현 : <math> | B \rangle = b_1 | A_1 \rangle + b_2 | A_2 \rangle + \cdots + b_N | A_N \rangle</math> (with <math>b_i = \langle B | A_i \rangle</math>) | ||
*기저의 선택에 따라 <math>b_i</math>의 값 달라짐 | *기저의 선택에 따라 <math>b_i</math>의 값 달라짐 | ||
*N개의 <math>b_i</math>들의 전개를 통한 벡터의 표현 : 예. <math>| Q \rangle = \begin{bmatrix}{ 1 \\ 5 \\ - {3 | *N개의 <math>b_i</math>들의 전개를 통한 벡터의 표현 : 예. <math>| Q \rangle = \begin{bmatrix}{ 1 \\ 5 \\ - {\frac{3}{2} } \end{bmatrix}</math> | ||
*벡터곱(내적) : <math>\ | *벡터곱(내적) : <math>\langle M | Q \rangle = m_1 q_1 + m_2 q_2 + \cdots </math> (기저에 따라 값이 달라지지 않음) | ||
*<math> | *(벡터 <math>| B \rangle</math>의 길이)<sup>2</sup> <math>= \langle B | B \rangle = \sum_i b_i^2</math> | ||
=== 연산자와 그것의 고유벡터 및 고유값 === | === 연산자와 그것의 고유벡터 및 고유값 === | ||
2025년 10월 3일 (금) 09:22 판
아래의 문헌을 요약한 것으로 2005년 물리학의 철학 수업 시간에 제출했던 발제문을 WikiNote에 옮긴 것임.
- Albert, D. Z. (1992), Quantum Mechanics and Experience. Harvard University Press.
- 발제문 : media:물리학의 철학_발제문_양자역학의 형식적 구조.hwp
문제제기 (중첩)
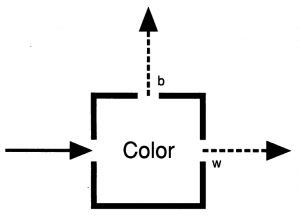
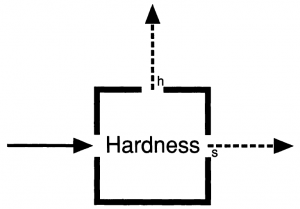
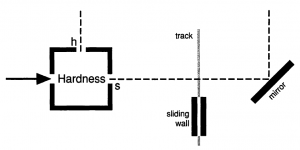
전자에 대해 색깔과 단단하기를 측정한다고 하자. 그리고 관측되는 색깔은 검은색과 흰색 두 종류만 있고, 관측되는 단단하기는 단단함과 부드러움 두 종류만 있다고 하자. 색깔을 측정하는 상자를 색깔상자, 단단하기를 측정하는 상자를 단단하기 상자라고 하자. 색깔 상자를 통해 흰색으로 측정된 전자는 반복해서 측정하더라도 항상 흰색으로 측정되며, 단단하기 상자를 통해 단단한 전자로 측정된 전자는 반복해서 측정하더라도 항상 단단한 전자로 측정된다.
- 첫 번째 문제제기
- 색깔 상자(그림 1.1)를 흰색으로 통과하고 단단하기 상자(그림 1.2)를 부드러움으로 통과한 전자를 다시 색깔상자에 통과시켜보면 검은색 또는 흰색으로 반반씩 나온다.
- → 색깔 또는 단단하기 상자의 통과가 다른 속성을 무작위로 흐트러뜨리는 영향을 주는 것처럼 보인다.
- 두 번째 문제제기
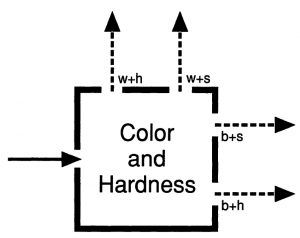
- 색깔과 단단하기를 동시에 측정하여 내보내는 상자(그림 1.3)를 만들 수 없다.
- → 측정은 한 번에 한 가지 속성만 가능한 것처럼 보인다.
- 세 번째 문제제기
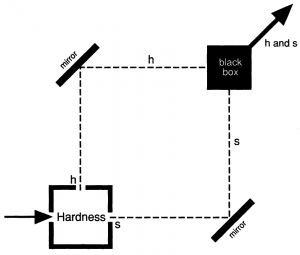
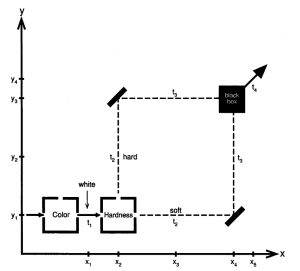
- 그림 1.4처럼 장치를 구성하고, 흰색으로 측정된 전자를 장치에 통과시키면 블랙박스에서 나온 h와 s에서는 정확히 흰색 전자만이 검출된다. 분명 단단하기 상자를 통과했으므로, 첫 번째 실험의 결과대로 무작위적인 색깔이 나와야 할 것 같으나 그렇지 않다.
- → 단단하기 상자를 통과한 전자는 단단함 경로로 갔거나 부드러움 경로로 갔을 것이고, 둘 중의 하나의 경로로 진행하는 전자는 색깔이 무작위여야 할 것이다. 그러나 그렇지 않다. 이는 첫 번째 실험 결과분석과 모순처럼 보인다.
- 한편, 그림 1.5처럼 한쪽 경로에 함정을 설치하면, 블랙박스에서 나온 h와 s에서는 정확히 반개의 전자만이 검출되며, 그 전자들의 색깔을 측정하면 정확히 검은색/흰색이 반반씩 측정된다. 또한, 두 경로에 모두 함정을 설치하면, 전자가 하나도 나오지 않는다.
- → 분명 전자는 두 경로 중 하나로 갔거나, 두 경로 모두로 갔거나, 두 경로 중 어느 곳으로도 가지 않았거나 넷 중에 하나일텐데, 이 실험은 네 경우 모두 아니라는 결론을 보여주는 듯하다.
→ 위의 실험결과는 모두 중첩이라는 현상 때문이다.
수학적 기초
벡터공간과 벡터
- 벡터 : 그것의 길이와 방향에 의해 특성화되는 수학적 객체. 벡터공간의 한 점.
- 벡터합 : 물리적 속성의 중첩과 대응.
- 수직(orthogonal) : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \langle A | B \rangle} = 0
- 벡터공간의 차원 : 직교벡터의 최대개수.
- N-차원 공간의 기저(basis) : N개의 직교단위(orthonormal) 벡터들.
- 기저를 이용한 벡터의 표현 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle | B \rangle = b_1 | A_1 \rangle + b_2 | A_2 \rangle + \cdots + b_N | A_N \rangle} (with 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_i = \langle B | A_i \rangle} )
- 기저의 선택에 따라 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_i} 의 값 달라짐
- N개의 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_i} 들의 전개를 통한 벡터의 표현 : 예. 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle | Q \rangle = \begin{bmatrix}{ 1 \\ 5 \\ - {\frac{3}{2} } \end{bmatrix}}
- 벡터곱(내적) : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \langle M | Q \rangle = m_1 q_1 + m_2 q_2 + \cdots } (기저에 따라 값이 달라지지 않음)
- (벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle | B \rangle} 의 길이)2 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle = \langle B | B \rangle = \sum_i b_i^2}
연산자와 그것의 고유벡터 및 고유값
- 연산자(operator) : 자기공간에서 이루어지는 벡터에서 벡터로의 사상(mapping). 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O \rangle B \rangle = | B' \rangle}
- 선형 연산자의 조건 : (a) 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O( | A \rangle + | B \rangle} , (b) 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O(c | A \rangle ) = c(O | A \rangle )}
- N-차원 공간의 선형 연산자의 표현 : N2 행렬로 표현 가능.
- 2차원의 경우, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O = \begin{bmatrix}O_{11} & O_{12} \\ O_{21} & O_{22} \end{bmatrix} (O_{ij} = \left< A_i | O | A_j \rangle}
)
- 예: 항등 연산자(unit operator) 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}} , 시계방향으로 90°회전시키는 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{bmatrix}0 & 1 \\ -1 & 0 \end{bmatrix}}
- 고유벡터와 고유값 : 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O}
에 대해 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O | B \rangle = @ | B \rangle}
의 조건을 만족하는 벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle | B \rangle}
와 상수 @.
- 위에서 벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle | B \rangle} 를 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O} 의 고유값 @인 고유벡터라고 한다.
양자역학의 5가지 원리
(A) 물리적 상태
- 물리계 - 벡터공간과 대응. (힐버트공간)
- 물리적 상태 - 길이가 1인 벡터와 대응. (1대1 대응은 아님. 예: 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| A \right>} 와 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle - \left| A \right>} 는 같은 상태를 표상)
(B) 관찰가능속성
관찰가능속성 - 특정한 조건을 만족하는 선형연산자와 대응. 만약, 어떤 물리적 상태를 표상하는 한 벡터가 어떤 관찰가능속성에 해당하는 연산자의 고유값 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a} 인 고유벡터이면, 그때의 그 관찰가능속성의 관측값은 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a} 이다. 한편, 연산자의 각 고유벡터들은 해당 관찰가능속성을 정확히 지닌 상태를 지칭하며, 벡터공간의 완전한 기저벡터들을 구성한다.
- hardness operator = 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}}
- 고유값 +1의 고유벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| hard \right> = \begin{bmatrix}1 \\ 0 \end{bmatrix}} (means precise hard)
- 고유값 -1의 고유벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| soft \right> = \begin{bmatrix}0 \\ 1 \end{bmatrix}} (means precise soft)
예2. 스핀 공간(2차원 벡터공간)에서의 색깔 속성의 표현
- color operator = 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}}
- 고유값 +1의 고유벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| black \right> = \begin{bmatrix} 1 \over \sqrt 2 \\ 1 \over \sqrt 2 \end{bmatrix}} (means precise black)
- 고유값 -1의 고유벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| white \right> = \begin{bmatrix}1 \over \sqrt 2 \\ - {1 \over \sqrt 2} \end{bmatrix}} (means precise white)
- 2차원 벡터공간을 양자역학에서는 스핀 공간이라 지칭한다.
서로 다른 연산자는 각각의 고유벡터들로 완전하면서 양립불가능한(incompatible) 기저를 구성한다. 물리적 상태에 해당하는 모든 벡터는 어떠한 (관찰가능속성에 해당하는) 연산자의 고유벡터이지만, 그 외의 다른 연산자의 고유벡터가 될 수는 없다. 즉, 한 연산자의 고유벡터는 다른 연산자의 고유벡터들의 합과 차로 표현된다. 위의 예를 이용해서 말하자면, 정확한(definite) 단단하기의 상태는 색깔속성의 두가지 상태가 중첩된 상태인 것이다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| hard \right> = \frac{1}{\sqrt 2} \left| black \right> + \frac{1}{\sqrt 2} \left| white \right>}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| soft \right> = \frac{1}{\sqrt 2} \left| black \right> - \frac{1}{\sqrt 2} \left| white \right>}
(C) 동역학
상태벡터는 슈뢰딩거 방정식을 따라 시간의 흐름에 따라 결정론적으로 변화한다.
- 상태벡터의 길이는 항상 1이므로 상태벡터는 시간에 따라 방향만 변화한다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_1 : \left| A \right> \to t_2 : \left| A' \right>} 이고, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_1 : \left| B \right> \to t_2 : \left| B' \right>} 이면, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_1 : \alpha \left| A \right> + \beta \left| B \right> \to t_2 : \alpha \left| A' \right> + \beta \left| B' \right> } 이다. (선형성)
(D) 실험과의 연결
현 상태벡터가 측정하려는 속성 연산자의 고유벡터라면 그것의 고유값이 바로 측정값이 될 테지만, 만약 현 상태벡터가 측정하려는 속성 연산자의 고유벡터가 아니라면 어떻게 될 것인가? 그것은 확률의 문제이다.
상태벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| A \right>} 의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 를 측정하는 상황에서, 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 에 대한 연산자의 고유벡터들이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| B = b _{1} \right> , \left| B = b _{2} \right> , \cdots , } ( 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_i} 는 각 고유값, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| B = b_i \right>} 는 고유값 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_i} 의 고유벡터) 이라고 할 때, 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 의 측정값이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_j} 일 확률은 아래와 같다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle P(B=b_j ) = \left( \left< a | B = b_j \right> \right)^2}
- 여기서 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| a \right>} 와 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle - \left| a \right>} 가 정확히 같은 물리적 상태를 표상한다는 점이 해명된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| soft \right> = \frac{1}{\sqrt 2} \left| black \right> - \frac{1}{\sqrt 2} \left| white \right>이므로,}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle P(Color=black) = \left( \left< soft | black \right> \right)^2 = \left( \frac{1}{\sqrt 2} \right)^2 = \frac {1}{2}}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle P(Color=white) = \left( \left< soft | white \right> \right)^2 = \left( - \frac{1}{\sqrt 2} \right)^2 = \frac {1}{2}}
(E) 붕괴
관찰가능속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O} 에 대해 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle O = @} 인 관측을 한 직후, 상태벡터는 고유값 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle @} 의 고유벡터로 “붕괴”한다.
양자역학의 예측 알고리즘
① 물리계에 표상하는 벡터공간 규정
② 다양한 관찰가능속성을 표상하는 연산자 규정
③ 현재 상태 측정
④ 나중 상태 예측 (원리 (C) 이용)
⑤ 측정 (원리 (E)에 따라 관측 가능한 고유상태 중 하나로 붕괴)
(⑤에서 ④의 과정 반복)
- 물음 : 원리 (C)는 항상 성립하는 원리. 원리 (E)는 측정 시에만 성립하는 원리. 그렇다면 (E)는 (C)의 특수한 경우로 보아야 할 것 같은데, 어떻게 보아야 할까?
복소 벡터공간으로의 확장
양자역학에서 사용되는 상태공간은 복소 벡터공간이다. 따라서 지금까지의 작업을 약간 수정할 필요가 있다.
벡터곱(내적)의 정의 변경
벡터 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| A \right>} 의 길이를 뜻하는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \sqrt {\left< A | A \right>}} 이 항상 양의 실수가 되도록 보장해줄 필요가 있다.
- 해결방법 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \sqrt {\left< A | A \right>} = a_1^* b_1 + a_2^* b_2 + \cdots} (구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a^*} 는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a} 의 켤레복소수)로 변경.
확률값
확률값이 항상 양의 실수가 되도록 보장해줄 필요가 있다.
- 해결방법 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle P(B=b_j ) = \left| \left< a | B = b_j \right> \right|^2} 로 변경.
- 이렇게 되면, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| A \right>} 는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle - \left| A \right>} 뿐만 아니라 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle @ \left| A \right>} (@는 절대값이 1인 복소수)와 똑같은 상태를 표상하게 된다.
속성 연산자
관측값을 뜻하는 연산자의 고유값이 실수가 되도록 보장해줄 필요가 있다.
- 해결방법 : 속성 연산자를 그것의 고유값이 실수로만 이루어진 Hermitian operator로만 한정.
- 연산자의 모든 고유값들은 실수이며, 관측값과 대응.
- N-차원 공간의 Hermitian operator는 N개의 직교 고유벡터 집합을 적어도 하나 가짐.
- 서로 다른 고유값에 대해 서로 다른 고유벡터 가지며, 각 고유값에 따른 길이 1의 고유벡터들은 공간의 유일한 기저를 형성. (이러한 연산자를 완전한 연산자라고 함)
- 임의의 Hermitian operator는 어떠한 측정가능속성과 대응.
- 임의의 벡터는 어떠한 Hermitian operator의 한 고유벡터.
- 모든 양자역학계는 무한한 상호 양립 불가능한 측정 가능 속성이 있다.
- 양립불가능의 정도에 대한 판단 : commutator 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle [A, B] = AB-BA} 의 값으로 판단 가능.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle [A,B]=0} 이면 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 와 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 는 적어도 하나 이상의 고유벡터를 공유하고 있음. 따라서 두 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 와 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 가 양립 불가능한 속성을 표상하기 위해서는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle [A,B] \neq 0} 이어야 한다.
좌표공간 (위치, 운동량과 같은 연속적이고 무한한 범위의 값을 가지는 물리량의 기술)
- ‘운동량’과 ‘위치’는 상호 양립 불가능한 관찰속성. 즉, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle [p,x] = i h \neq 0} .
- 운동량 또는 위치에 관한 상태를 기술하기 위한 조건.
무한차원의 상태공간과 상태벡터
- 일차원 공간에서의 위치 연산자를 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle X} 라 하면, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle X} 의 고유값들은 연속적이면서 그 범위는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle (-\infty , \infty)} .
- 즉, 평범한 일차원의 공간을 표상하기 위한 상태공간은 무한차원공간이어야 한다..
- 흔히, 위처럼 무한차원의 상태공간에서의 상태벡터를 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi \right>} 라 지칭한다.
구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi \right>} 를 연산자 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle X} 의 무한한 고유벡터들을 기저로 삼아 표현하면 아래와 같다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi \right> = a_5 \left| X=5 \right> + a_7 \left| X=7 \right> + a_{72.93} \left| X=72.93 \right> + \cdots} (where 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_x = \left< \Psi | X=x \right>} )
파동함수
- 위의 표현과 동등하게 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle (-\infty , \infty)} 의 정의역을 갖고 그 함수값으로 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_x} 를 갖는 함수 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi (x)} 를 생각할 수 있다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi (x) = \left< \Psi | X=x \right> = a_x} (흔히 이 함수가 파동함수의 형태를 갖기 때문에 파동함수라고 부름)
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi \right> = \frac{1}{\sqrt 2} \left| X=1 \right> + \frac{1}{\sqrt 2} \left| X=-1 \right>} 를 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi (x)} 로 표현하면,
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi (x) = \begin{cases} \frac{1}{\sqrt2} \quad (x=1) \\ \frac{1}{\sqrt2} \quad (x=-1) \\ 0 \quad (x \neq 1 \& x \neq -1 ) \end{cases}}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle P(X=x_j ) = \left| \Psi (x_j ) \right)^2}
2개 이상의 입자로 구성된 계
두 입자로 구성된 계의 상태벡터와 상태공간
1번 입자의 상태벡터가 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi_a \right>} , 2번 입자의 상태벡터가 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi_b \right>} 일 때, 입자쌍의 상태벡터는 보통 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi_a \right>_1 \left| \Psi_b \right>_2} 또는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi_a^1 , \Psi_b^2 \right>} 로 표현된다.
1번 입자와 2번 입자 각각의 상태가 N차원의 상태공간에서 기술될 때, 두 입자쌍의 상태는 새롭게 구성된 N2차원의 상태공간에서 기술된다. 이 때 새롭게 구성된 상태공간의 기저는 두 입자의 상태공간의 각 기저벡터들 간의 텐서곱에 의해 만들어지는 N2개의 직교단위벡터들에 의해 구성된다.
새로운 기저벡터들 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi_a^1 , \Psi_b^2 \right>} for 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle i , j = 1 , 2, \cdots , N} (구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi_i} 와 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \Psi_j} 는 원래의 기저벡터들).
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left< \Psi_i^1 , \Psi_j^2 \middle| \Psi_k^1 , \Psi_l^2 \right> =0} unless 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle i=k \text{ & } j=k} (where 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left< \Psi_i^1 , \Psi_j^2 \middle| \Psi_k^1 , \Psi_l^2 \right> =\left< \Psi_i^1 \middle| \Psi_k^1 \right> \left< \Psi_j^2 \middle| \Psi_l^2 \right>} )
- 즉, 새로운 기저벡터들간의 벡터곱(내적)은 원리적으로 0.
이제 새로운 상태공간에서 두 입자로 구성된 계의 상태는 일반적으로 다음과 같이 표현된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi^{1,2} \right> = a_{11} \left| \Psi_1^1 , \Psi_1^2 \right> + a_{12} \left| \Psi_1^1 , \Psi_2^2 \right> + \cdots + a_{ij} \left| \Psi_i^1 , \Psi_j^2 \right> + \cdots}
위의 일반적인 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi^{1,2} \right>} 는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \Psi^1 \right> \left| \Psi^2 \right>} 의 꼴로 표현 가능한 상태와 표현 불가능한 상태로 나뉘어진다. 이는 아래의 분리가능성의 문제를 낳는다.
분리 가능성과 분리 불가능성
분리 불가능한 상태
두 입자의 상태가 아래와 같다고 해보자.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right> = \frac{1}{\sqrt2} \left| \Psi_1^1 , \Psi_1^2 \right> + \frac{1}{\sqrt2} \left| \Psi_2^1 , \Psi_2^2 \right>}
위의 상태벡터는
- 1번 입자의 상태 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right> = \frac{1}{\sqrt2} \left| \Psi_1 \right> + \frac{1}{\sqrt2} \left| \Psi_2 \right>}
- 2번 입자의 상태 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^2 \right> = \frac{1}{\sqrt2} \left| \Psi_1 \right> + \frac{1}{\sqrt2} \left| \Psi_2 \right>}
로 분리될 수 없다. 두 입자의 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right>} 를 보고, 1번 입자의 상태는 이러이러하고 2번 입자의 상태는 저러저러하다고 말할 수 없다. 두 입자의 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right>} 가 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right>\left| Q^2 \right>} 의 꼴로 표현될 수 없는 경우, 그 상태를 분리 불가능한 상태라고 한다.
분리 가능한 상태
두 입자의 상태가 아래와 같다고 해보자.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right> = \frac{1}{2} \left| \Psi_1^1 , \Psi_1^2 \right> + \frac{1}{2} \left| \Psi_2^1 , \Psi_1^2 \right> + \frac{1}{2} \left| \Psi_2^1 , \Psi_2^2 \right>}
위의 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right>} 는 아래의 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right>} 과 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^2 \right>} 의 텐서곱 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right> \left| Q^2 \right>} 로 정확히 표현된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right> = \frac{1}{\sqrt2} \left| \Psi_1^1 \right> + \frac{1}{\sqrt2} \left| \Psi_2^1 \right>}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^2 \right> = \frac{1}{\sqrt2} \left| \Psi_1^2 \right> + \frac{1}{\sqrt2} \left| \Psi_2^2 \right>}
이 경우 우리는 1번 입자의 상태는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right>} , 2번 입자의 상태는 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^2 \right>} 라고 말할 수 있다.
즉, 두 입자의 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right>} 가 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q^1 \right> \left| Q^2 \right>} 의 꼴로 표현 가능한 경우, 그 상태를 분리 가능한 상태라고 한다.
측정
두입자의 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| k \right>} 에서, 1번 입자의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 의 측정값이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_i} 이고 2번 입자의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle B} 의 측정값이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle b_j} 일 확률은
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \left< A^1 = a_i , B^2 = b_j | k \right> \right|^2}
만약, 1번 입자의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 의 측정값이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_i} 일 확률은
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| \left< A^1 = a_i , L^2 = l_1 | k \right> \right|^2 + \left| \left< A^1 = a_i , L^2 = l_2 | k \right> \right|^2 + \cdots + \left| \left< A^1 = a_i , L^2 = l_j | k \right> \right|^2 + \cdots}
4) 붕괴
실제로 1번 입자의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 를 측정하여 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_5} 가 측정됐다면, 측정직후의 상태는 어떻게 될까?
- 원래상태 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| k \right> = \sum_{i, j} d_{ij} \left| A^1 = a_i , B^2 = b_j \right>}
- 측정 후 : 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| k' \right> = \alpha \sum_{j} d_{5j} \left| A^1 = a_5 , B^2 = b_j \right>} (where 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \alpha = \frac{1}{\sum_j d_{5j}}} )
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| k \right> = \frac{1}{\sqrt3} \left| A^1 = a_1 , B^2 = b_2 \right> + \frac{1}{\sqrt3} \left| A^1 = a_1 , B^2 = b_{27} \right> + \frac{1}{\sqrt3} \left| A^1 = a_8 , B^2 = b_{38} \right>} 일 때,
- 1번 입자의 속성 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle A} 의 측정값이 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle a_1} 라고 하자. 이 때, 측정후의 상태는 아래와 같이 붕괴한다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| k \right> = \frac{1}{\sqrt2} \left| A^1 = a_1 , B^2 = b_2 \right> + \frac{1}{\sqrt2} \left| A^1 = a_1 , B^2 = b_{27} \right>}
5) 자유도
자유도 : 한 계를 명세하기 위해 M개의 독립적인 물리속성이 필요한 경우, 그 계는 M의 자유도를 가졌다고 한다. 예를 들어, x방향 위치 속성, y방향 위치 속성, z방향 위치 속성, 스핀 속성은 한 입자가 가진 독립적 속성들이다. 3차원 좌표공간에서 자유롭게 움직일 수 있고 자유로운 스핀값을 가지는 입자 하나로 구성된 물리계의 자유도는 4이다.
한편, 두 입자로 이루어진 계의 상태공간이 각 입자의 상태공간의 텐서곱으로 구성되듯, 한 입자로 이루어진 계의 상태공간 또한 여러 독립적인 상태공간의 텐서곱으로 구성된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \{ \left| SPIN = spin_i \right> \left| \Psi_x = x_j \right> \left| \Psi_y = y_k \right> \left| \Psi_z = z_l \right> : i=1 \text{ or } 2, \; j, k, l \in {\mathbb R} \}}
예2. 위의 상태공간에서의 일반적인 상태벡터 표현
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q \right> = \sum_{i,j,k,l} a_{ijkl} \left| SPIN = spin_i \right> \left| \Psi_x = x_j \right> \left| \Psi_y = y_k \right> \left| \Psi_z = z_l \right> }
5. 두-경로 실험에 대한 표준적인 해석
1) 두-경로 실험에서 장치를 통과한 전자는 왜 모두 흰색으로 측정되는가?
구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_1} 에서의 상태
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{split} \left| Q_{t_1} \right>&= \left| white, X=x_1 , Y=y_1 \right> \\ & = \frac{1}{\sqrt {2}} \left| hard \right> \left| X=x_{1} ,Y=y _{1} \right>+\frac{1}{\sqrt {2}} \left| soft \right> \left| X=x _{1} , Y=y _{1} \right> \\ & = \frac{1}{\sqrt {2}} \left| a \right>+ \frac{1}{\sqrt {2}} \left| b \right> \end{split} }
구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_2} 에서의 상태
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q_{t_2} \right> = \frac{1}{\sqrt {2}} \left| hard \right> \left| X=x_{2} ,Y=y _{2} \right>+\frac{1}{\sqrt {2}} \left| soft \right> \left| X=x _{3} , Y=y _{1} \right>}
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_2} 의 시점에서, 전자가 두 경로 중 어디에 있느냐고 묻는 것 자체가 의미 없는 질문이다. 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_2} 에서의 전자의 상태는 두 상태의 중첩으로 표현될 뿐이다.
구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 에서의 상태
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \begin{split} \left| Q_{t_2} \right> & = \frac{1}{\sqrt {2}} \left| hard \right> \left| X=x_{5} ,Y=y _{4} \right>+\frac{1}{\sqrt {2}} \left| soft \right> \left| X=x _{5} , Y=y _{4} \right> \\ & = \frac{1}{\sqrt {2}} ( \left| hard \right> - \left| soft \right> ) \left| X=x_{5} ,Y=y _{4} \right> \\ & = \left| white, X=x_5 , Y=y_4 \right> \end{split} }
중간 시점에서의 측정이 미치는 효과
만약 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_2} 에서 전자의 위치를 측정한다면, 중첩상태는 사라지고, 아래처럼 둘 중 하나의 상태로 붕괴한다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| hard \right> \left| X=x_2 , Y=y_2 \right> \text{ or } \left| soft \right> \left| X=x_3 , Y=y_1 \right> }
둘 중 하나가 관측될 확률은 1/2이며, 이대로 가면 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 에서의 상태는 아래의 두 상태 중 하나가 된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q_{t_4} \right> = \left| hard , X=x_5 , Y=y_4 \right> \text{ or } \left| soft , X=x_5 , Y=y_4 \right> }
따라서 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 시점에 색깔을 측정하면 검은색과 흰색이 반반씩 측정된다.
함정 설치가 미치는 효과
만약, 경로 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle y_1 , x_3 } 에 함정을 설치하면, 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 에서의 상태는 아래와 같다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q_{t_4} \right> = \frac{1}{\sqrt2} \left| hard \right> \left| X=x_5 , y=y_4 \right> + \frac{1}{\sqrt2} \left| soft \right> \left| X=x_3 , y=y_1 \right>}
따라서 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 에 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle (x_5 , y_4 )} 지점에서 전자가 검출될 확률은 1/2이며, 그 때의 전자는 단단한 전자일 것이다. 따라서 그 지점에서 색깔을 측정하면 검은색과 흰색이 반반씩 측정될 것이다.
아무것도 아닌(total-of-nothing) 상자의 효과
상자의 구현 : 상태 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| A \right>} 의 입자가 들어오면 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle - \left| A \right>} 의 상태로 바꾸어 내보내는 방식으로 구현한다.
보통의 경우, 입자의 관측가능속성은 하나도 바뀌지 않는다. 그러나, 위의 실험에서 중첩상태 중 한 경로에만 상자를 설치하면, 재밌는 변화가 일어난다. 예를 들어, 경로 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle (x_{3.5} , y_1 )} 에 이 상자를 설치하면 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_3 } 에서의 상태는 아래와 같이 된다.
- 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle \left| Q_{t_3} \right> = \frac{1}{\sqrt2} \left| hard \right> \left| X=x_3 , Y=y_3 \right> + \frac{1}{\sqrt2} \left| soft \right> \left| X=x_4 , Y=y_2 \right>}
그리고 구문 분석 실패 (MathML을 사용하되 미지원 시 SVG나 PNG 사용 (최신 브라우저나 접근성 도구에 권장): "https://en.wikipedia.org/api/rest_v1/" 서버에서 잘못된 응답 ('Math extension cannot connect to Restbase.'):): {\displaystyle t_4} 에 이르렀을 때 그 상태는
- 구문 분석 실패 (알 수 없는 함수 "\begin{split}"): {\displaystyle \begin{split} \left| Q_{t_4} \right> &= \frac{1}{\sqrt2} ( \left| hard \right> + \left| soft \right> ) \left| X=x_5 , Y=y_4 \right>\\ &= \left| black , X=x_5 , Y=y_5 \right> \end{split} }
- 가 되어, 색깔이 검은색으로 바뀌어버린다.
관련 항목
- 물리학의 철학(수업)
- Ismael, Jenann, "Quantum Mechanics", Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy.