"발산 (벡터 연산자)"의 두 판 사이의 차이
imported>Zolaist |
|||
| 3번째 줄: | 3번째 줄: | ||
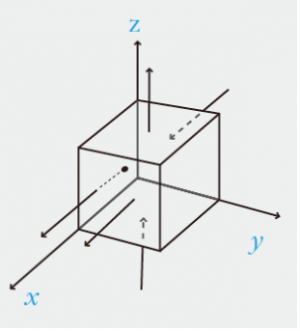
[[그림:발산.png|thumb]]다음의 그림은 발산의 의미를 이해하는 데 도움이 될 것이다. 이 그림은 각 변의 길이가 1인 단위 입방체의 각 면에 들어오고 나가는 유량이 튜브(화살표)의 개수로 그려져 있다. 이 단위 입방체에서 유량의 발산은 다음과 같이 대략 계산될 수 있다. | [[그림:발산.png|thumb]]다음의 그림은 발산의 의미를 이해하는 데 도움이 될 것이다. 이 그림은 각 변의 길이가 1인 단위 입방체의 각 면에 들어오고 나가는 유량이 튜브(화살표)의 개수로 그려져 있다. 이 단위 입방체에서 유량의 발산은 다음과 같이 대략 계산될 수 있다. | ||
:<math>\begin{ | :<math>\begin{align} | ||
\nabla \cdot \mathbf {v} &= \frac {\partial v_x }{\partial x} + \frac {\partial v_y }{\partial y}+\frac {\partial v_z }{\partial z} \\ | \nabla \cdot \mathbf {v} &= \frac {\partial v_x }{\partial x} + \frac {\partial v_y }{\partial y}+\frac {\partial v_z }{\partial z} \\ | ||
&\simeq \frac {\Delta v_x }{\Delta x} + \frac {\Delta v_y }{\Delta y}+\frac {\Delta v_z }{\Delta z} \\ | &\simeq \frac {\Delta v_x }{\Delta x} + \frac {\Delta v_y }{\Delta y}+\frac {\Delta v_z }{\Delta z} \\ | ||
&= (2-1) +(0-0)+(1-1) \\ | &= (2-1) +(0-0)+(1-1) \\ | ||
&= 1 | &= 1 | ||
\end{ | \end{align}</math> | ||
즉 입방체에 들어오는 유체는 튜브 두 개를 통해 들어오지만, 입방체에서 나가는 유체는 총 세 개의 튜브를 통해 나가고 있으므로, 입방체 내에는 튜브가 시작되는 한 개의 공급원이 있어야 하는 것이다. | 즉 입방체에 들어오는 유체는 튜브 두 개를 통해 들어오지만, 입방체에서 나가는 유체는 총 세 개의 튜브를 통해 나가고 있으므로, 입방체 내에는 튜브가 시작되는 한 개의 공급원이 있어야 하는 것이다. | ||
2021년 7월 13일 (화) 02:17 기준 최신판
맥스웰이 고안한 유체 시스템의 유체 흐름과 공급원 및 배수구 사이의 관계는 ‘발산’이라는 벡터 연산자를 이용하면 간편하게 표현된다. 이는 유체 시스템과 같은 벡터장 내 임의의 지점에서 나오는 유량과 그 지점으로 들어가는 유량의 차이를 나타내는 벡터 연산자로서, 각 지점의 공급량(배수량은 음의 공급량)을 구하는 데 사용된다. 수학적인 기호를 이용하면, 로 정의된 벡터장 내 각 지점의 발산은 로 표현되며, 그 값은 의 각 성분에 대한 편미분(즉, 성분별 증가분)의 합으로 구성된 다음의 스칼라량으로 정의된다.
다음의 그림은 발산의 의미를 이해하는 데 도움이 될 것이다. 이 그림은 각 변의 길이가 1인 단위 입방체의 각 면에 들어오고 나가는 유량이 튜브(화살표)의 개수로 그려져 있다. 이 단위 입방체에서 유량의 발산은 다음과 같이 대략 계산될 수 있다.
즉 입방체에 들어오는 유체는 튜브 두 개를 통해 들어오지만, 입방체에서 나가는 유체는 총 세 개의 튜브를 통해 나가고 있으므로, 입방체 내에는 튜브가 시작되는 한 개의 공급원이 있어야 하는 것이다.
이러한 수학적 직관을 통해, 맥스웰은 전자기장을 기술하는 방정식에서 형태의 수학적 표현이 등장하면 그것의 물리적 의미를 쉽게 해석할 수 있었다. 그래서 전기력선의 발산은 전기력선의 생성량으로서 전하량을 의미했으며, 자기력선의 발산은 자기력선의 생성량으로서 자유 자극의 양을 의미했다.
발산 정리
압축 불가능한 유체 시스템과 같은 벡터장에서, 임의의 지점의 (단위 면적당) 유량()의 발산()이 그 지점의 공급 밀도()를 나타낼 경우(), 임의의 크기를 가진 공간의 표면을 통해 빠져나가는 총유량()은 그 내부의 총 공급량()과 같다. 즉 이를 수학적으로 표현한 것이 다음의 발산 정리이다.
- if
- then
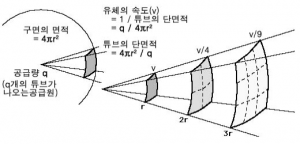
이 발산 정리를 이용하면, 총공급량 의 점 공급원과 그로부터 무한대의 거리에 총배수량 의 배수구들이 사방으로 배치된 시스템에서, 공급원으로부터의 거리 에 따른 유체의 속도 는 아래와 같이 구해진다.
- (∵ 반지름 인 구면의 면적은 )
관련 항목
- 기울기 (벡터 연산자) ()
- 회전 (벡터 연산자) ()
- 정동욱, 뉴턴의 품에 들어온 ‘힘의 선’ (『패러데이 & 맥스웰』, 만남 4)