공간이란 무엇인가

공간이란 무엇일까? 라이프니츠의 관계론에 따르면, 공간이란 물체들 사이에 성립하는 ‘위쪽’, ‘동쪽’ 따위의 상대적 위치 관계의 총합으로, 물체들이 없으면 공간도 존재하지 않는다. 반면 뉴턴의 실체론에 따르면, 공간은 용기와 같은 실체로서 물체들 간의 상대적 위치 관계로 환원되지 않는 무엇으로, 물체들이 전부 사라졌다고 해도 공간은 존재한다. 공간의 형이상학, 즉 공간의 존재론적 지위에 대한 물음은 과학과 철학의 경계선에 있는 문제이다. 이 질문은 순수히 철학적일 수 없는데, 왜냐하면 그에 대한 답은 물리학의 내용과 밀접한 관련을 맺고 있기 때문이다. 또한 이 질문은 순수히 과학적일 수도 없는데, 왜냐하면 경험적 탐구만으로는 이에 답할 수 없기 때문이다. 즉 이 논쟁은 과학과 철학 사이에 뚜렷한 경계선이 없다는 것을 보여준다.

뉴턴의 실체론 : 절대 운동은 절대 공간에 대한 운동

뉴턴의 실체론은 운동에 대한 고찰로부터 등장했다. 뉴턴은 운동이 정의되려면 기준이 필요하다고 생각했다. 상대 운동이란 다른 물체를 기준으로 한 물체의 위치 변화이다. 예컨대 돌이 지상으로 떨어질 때, 지구를 기준으로 삼으면 돌이 운동 중이지만, 돌을 기준으로 삼으면 지구가 돌을 향해 운동 중이다. 그러나 이들 중 진짜 운동 중인 것은 무엇인가? 뉴턴은 진짜 운동, 즉 ‘절대 운동’이 있다고 믿었는데, 이를 위해서는 절대 운동의 기준도 필요했다. 뉴턴에 따르면, 그 기준은 바로 공간 그 자체로, 뉴턴은 이를 ‘절대 공간’이라고 불렀다. 뉴턴에 따르면, 모든 물체는 절대 공간 안에서 특정한 위치에 있는데, 이 절대 위치가 시간에 따라 변하는 물체는 ‘절대 운동’을 하고 있는 것이다.

라이프니츠의 관계론 : 절대 공간은 공허한 개념

라이프니츠는 상대 운동과 구별되는 절대 운동이 존재한다는 점에는 동의했지만, 그는 절대 운동을 “변화의 직접적인 원인이 물체 자체에 있는 운동”으로만 정의했다. 그는 절대 운동을 절대 공간과 연관시키지 않았는데, 왜냐하면 절대 공간은 경험적 차이를 낳을 수 없는 공허한 개념처럼 보였기 때문이다. 이를 보이기 위해 라이프니츠는 절대 공간을 가정하여 다음의 두 우주를 상상할 것을 주문한다. 우주 U1에서는 물체들이 절대 공간에서 저마다의 절대 속도로 운동 중이고, 그와 동일한 물체들이 담긴 우주 U2에서 물체들 사이의 현재 상대 위치는 U1과 동일하고 물체들의 절대 속도는 항상 U1에서의 절대 속도보다 동쪽 방향으로 20m/s씩 증가해 있다. 그렇다면 U1과 U2 속 물체들의 상대 위치와 상대 운동은 항상 같기 때문에, 어떠한 실험과 관찰도 우리가 둘 중 어느 우주에 사는지 구별해 주지 못할 것이다. 이에 따라 라이프니츠는 U1과 U2가 동일한 우주이며, 절대 공간 개념은 불필요하다고 주장했다. 결국 라이프니츠에게 공간 상의 위치 변화는 상대적일 뿐이기에, 진정한 운동, 즉 절대 운동이란 절대 공간과의 관계를 통해 정의되기보다 물체 내부의 원인에 기인한 운동으로 정의되었던 것이다.

뉴턴의 양동이 사고 실험 : 절대 공간의 필요성

뉴턴의 양동이 사고실험. 출처 : 오카샤 (2017).

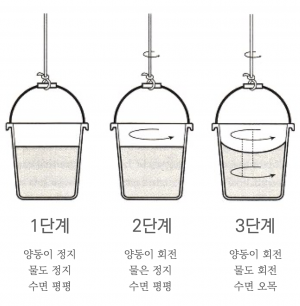
라이프니츠의 비판에 대응하여 뉴턴은 양동이 사고 실험을 통해 절대 공간이 경험적 차이를 낳는 경우가 존재한다고 주장했다. 그는 물이 채워진 양동이가 끈에 매달려 있는 모습을 상상할 것을 주문한다. 실험을 시작할 때는 양동이도 물도 멈춰 있으며 수면도 평평하다(1단계). 끈을 여러 번 꼬았다가 놓으면 양동이가 돌기 시작하는데, 처음에는 양동이만 돌고 그 안의 물은 가만히 있고 수면도 평평하다(2단계). 하지만 얼마 후에는 양동이의 운동이 물에 전달되어 물도 양동이와 나란히 돌게 되며, 이때는 물이 가장자리로 쏠리면서 수면이 오목해진다(3단계). 3단계에서 수면이 오목해진 원인은 무엇일까? 우리는 물의 회전 운동 때문이라고 답하고 싶을 것이다. 그러나 물의 회전 운동은 무엇을 기준으로 한 회전 운동일까? 3단계에서 물은 양동이와 나란히 돌고 있으므로, 즉 물과 양동이는 서로에 대해 정지 상태에 있으므로, 양동이는 물의 회전 운동의 기준이 될 수 없다. 뉴턴에 따르면, 물의 회전 운동의 기준이 될 수 있는 것은 절대 공간뿐이며, 수면이 오목해진 원인은 바로 절대 공간에 대한 물의 회전이다. 결국 이 사례에서 절대 공간은 경험적 차이를 낳는다. 절대 공간을 도입하지 않고는 1단계와 3단계에서 관찰되는 수면의 모양 차이를 설명할 수 없어 보이기 때문이다.

그런데 절대 공간에 대한 물의 회전 운동은 어떻게 수면을 오목하게 만드는가? 뉴턴은 이를 관성 효과로 설명할 수 있었다. 그의 운동 이론에 따르면, 모든 물체는 자신의 운동 상태를 유지하려는 관성을 가지고 있으며, 그 운동 방향이나 속력이 변화하는 가속 운동 중에는 ‘관성 효과’가 관측된다. 예를 들어, 버스가 갑자기 출발할 때 정지해 있던 승객은 계속 정지해 있으려는 경향 때문에 뒤로 밀리고, 원을 그리며 회전하는 물은 매순간 접선 방향의 운동을 유지하려고 하기에 양동이의 가장자리로 쏠리면서 오목한 모양의 수면을 만들어낸다. 이러한 관성 효과들은 물체가 절대 공간에 대해 가속 운동 중일 때에만 관측되는 현상으로, 버스가 계속 정지해 있거나 물이 회전하지 않으면 일어나지 않는다. 즉 뉴턴은 절대 공간에 대한 물체의 위치와 속도는 탐지할 수 없더라도, 절대 공간에 대한 물체의 가속도는 탐지할 수 있다고 말하고 있는 것이다.

마흐의 사변

그러나 뉴턴의 논변에도 빈틈은 있었다. 19세기의 과학자 마흐는 가속 중인 물체에 작용하는 ‘관성 효과’가 우주의 다른 물체들의 양과 분포에 의한 것일지도 모른다고 생각했다. 이러한 사변에 기초하여 그는 관성을 절대 공간이 아니라 다른 물체들과의 관계를 통해 정의하기 위해 노력했고, 그 결과 그는 뉴턴의 제1법칙을 대체하는 다음의 법칙을 제안하기도 했다.

${\frac {d^{2}{\frac {\sum mr}{\sum m}}}{dt^{2}}}=0$ (마흐의 법칙)

이러한 사변의 연상선상에서, 그는 뉴턴의 양동이 속의 물이 지구와 별들 따위의 다른 물체들을 기준으로도 회전 중이라는 점에 주목했다. 어쩌면 그러한 다른 물체들이 없었다면 양동이 속의 물은 오목한 수면을 만들어내지 않았을 수도 있을 것이다. 즉 그는 양동이 속의 물을 오목하게 만든 것은 절대 공간에 대한 회전이 아니라 지구와 별들에 대한 회전일 수도 있다고 주장한 것이다. 관찰은 뉴턴의 설명과 자신의 대안적 설명을 모두 허용한다. 그런데 그의 말대로 물체들 사이의 상대적 위치 관계만 중요하다면, 물이 담긴 양동이가 가만히 있고 지구와 별들이 양동이를 기준으로 회전하더라도 수면이 오목해져야 한다. 마흐는 정말로 그럴 것이라고 생각했지만, 이는 관성 개념에 기초한 뉴턴의 역학 이론이 참이라면 불가능했다. 따라서 마흐에게는 지구와 별이 정지한 가운데 물이 담긴 양동이가 도는 우주든, 물이 담긴 양동이가 정지한 가운데 지구와 별이 도는 우주든, 동일한 관찰 귀결을 낳는 새로운 역학 이론이 필요했다.

아인슈타인의 등가 원리

등가 원리

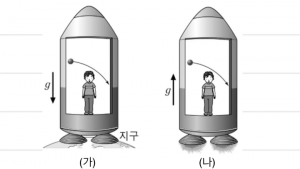
아인슈타인은 마흐의 요구를 '마흐의 원리'라 부르면서, 그에 부합하는 새로운 역학 이론을 고안하고자 했다. 아인슈타인의 등가 원리에 따르면, 가속 운동을 하는 물체에서 나타나는 관성 효과는 다른 물체에 의한 중력 효과와 국소적으로는 구별 불가능하다. 예컨대 그림의 (가)처럼 지구 위에 가만히 정지해 있는 로켓 내에서 물체들은 지구의 중력에 의해 g의 가속도로 자유 낙하한다. 그런데 (나)처럼 우주에서 g의 가속도로 상승 중인 로켓 내에서도 물체들은 (가)와 마찬가지로 g의 가속도로 낙하하는 것처럼 보일 것이다. 이처럼 관성 효과와 중력 효과는 구별 불가능하며, 아인슈타인은 가속 운동에 의한 관성 효과가 때로는 다른 물체들에 의한 중력 효과로 치환될 수 있다고 생각했다. 그렇다면 (나)에서 나타나는 관성 효과는 무엇인가? 로켓 내부의 관찰자의 입장에서, 그것은 정지해 있는 로켓 외부의 모든 물체들이 아래로 가속 운동함에 따라 형성된 중력의 결과일 수도 있는 것이다.

등가 원리에 기초한 아인슈타인의 일반상대성 이론은 관성 효과를 (가속 운동 중인) 다른 물체에 의해 형성된 중력을 통해 설명할 수 있는 길을 열어줌으로써 마흐의 원리를 구현한 것처럼 보인다. 틀-끌림(Frame-Dragging) 효과에 대한 이론적 예측과 경험적 입증은 그 증거로 간주되기도 한다. 그러나 여러 학자들의 지적에 따르면, 일반상대성 이론은 마흐의 원리를 완벽하게 구현하고 있지 않다. 왜냐하면 일반상대성 이론에서 물체를 제거하면 중력장이 제거되는 것이 아니라 아인슈타인이 없애고자 했던 유사 절대 공간과 같은 초기 중력장이 남기 때문이다. 그래서 일반상대성 이론 하에서는 다음과 같은 모형들이 가능하다. 첫째, 일반상대성 이론은 다른 물체가 없는 빈 공간에서 자신의 연료를 분사하며 가속 운동하는 로켓에 대한 모형을 허용한다. 로켓 바깥에서 가속 운동 중인 물체들에 의한 중력 효과만으로는 로켓 내부의 현상을 설명 불가능한 경우가 있다는 것이다. 만약 로켓 내부의 관찰자의 입장에서 이를 묘사하려면, 아래 방향으로 중력이 작용하는 초기 중력장을 가정해야 한다. 물론 이는 균일한 초기 중력장 하에서 로켓이 가속 운동 중이라는 묘사와 동등하다. 그러나 두 묘사 중에서 우리는 후자의 묘사를 선호하는 편이며, 그러한 선호는 마치 절대 공간을 상정하는 것과 유사하다. 둘째, 마흐의 원리는 다른 물체가 없는 공간에서 회전하는 물체를 허용하지 않지만, 일반상대성 이론은 다른 물체가 없는 공간에서 회전하는 물체에 대한 모형을 허용한다.

참고문헌

• 오카샤, 사미르 (2017), 「물리학, 생물학, 심리학 분야의 철학적 문제들」, 『과학철학』, 파주: 교유서가, 6장.
• Huggett, Nick (2015), Absolute and Relational Theories of Space and Motion, Stanford Encyclopedia of Philosophy.
• Mach, Ernst (1919), The Science of Mechanics: A Critical and Historical Account of Its Development, 4th edition, tr. Thomas J. McCormack, Chicago and London: The Open Court Publishing Co.
• Rynasiewicz, Robert (2011), Newton’s Views on Space, Time, and Motion, Stanford Encyclopedia of Philosophy.

더 읽을거리

아인슈타인의 특수상대성 이론과 일반상대성 이론 발견 과정에 대해서는 아래의 글들을 참고하라.

• Norton, John D., From the Magnet and Conductor to the Relativity of Simultaneity
• Norton, John D., Einstein's Pathway to General Relativity
• 피터 갤리슨 지음, 정동욱 옮김, 「아인슈타인의 시계들: 시간의 장소」, 박민아, 김영식 편, 『프리즘: 역사로 과학 읽기』 (서울: 서울대학교출판부, 2007), 247-295쪽.

아인슈타인의 일반상대성 이론이 마흐의 원리에 부합하는지에 대한 논의는 아래의 문헌을 참고하라.

• Barbour, J. and H. Pfister (Eds.) (1995). Mach’s Principle: From Newton’s Bucket to Quantum Gravity. Birkhäuser.
• Lichtenegger, Herbert and Bahram Mashhoon (2007), Mach's Principle, in L. Iorio (ed.), The Measurement of Gravitomagnetism: A Challenging Enterprise, New York: Nova Science, pp. 13-25.

일반상대성 이론이 관계론을 지지한다고 주장하는 ‘구멍 논변’에 대해서는 아래의 문헌을 참고하라.

• Norton, John D. (2019), The Hole Argument, Stanford Encyclopedia of Philosophy.
• 천현득 (2010), “시공간의 본성에 대하여 : 구멍 논변을 중심으로”, 『과학철학』 13(2), 147-172쪽.