케플러의 법칙이란 요하네스 케플러(Johannes Kepler, 1571-1630)가 발견한 행성 운동에 관한 세 가지 법칙을 의미하며, 각각의 법칙은 "타원 궤도 법칙"(제1법칙), "면적 속도 일정의 법칙"(제2법칙), "조화의 법칙"(제3법칙)이라는 애칭을 가지고 가지고 있다. 제1법칙과 제2법칙은 1609년에 출판한 『새로운 천문학(New Astronomy; Astronomia nova)』에 함께 등장했으며, 제3법칙은 1619년에 출판한 『우주의 조화(Harmonies of the World; Harmonices Mundi)』에 등장했다. 이 법칙들과 (법칙들에 근거해 제작된) 『루돌프 천문표(Rudolphine Tables; Tabulæ Rudolphinæ)』(1627)는 행성의 위치에 대한 예측의 정확성을 극도로 향상시켰으며, 그 덕분에 케플러의 법칙에 전제된 코페르니쿠스의 태양중심설은 천문학자들 사이에서 널리 인정받게 되었다. 또한 이 법칙들은 뉴턴이 만유인력의 법칙을 발견하고 뒷받침하는 데도 기여함으로써, 코페르니쿠스의 『천구의 회전에 관하여』로부터 시작되어 뉴턴의 『프린키피아』에 의해 완결되는 코페르니쿠스 혁명의 가장 중요한 징검다리가 되었다.
케플러의 법칙은 아래의 세 가지 법칙으로 구성되어 있으며, 그 발견 과정에는 정밀한 관측과 복잡한 수학이 필요했다.
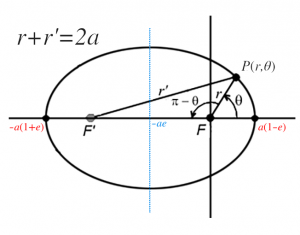
- 제1법칙(타원 궤도 법칙) : 행성은 태양을 한 초점으로 하는 타원궤도를 그리면서 공전한다.
- 제2법칙(면적 속도 일정의 법칙) : 행성과 태양을 연결하는 가상적인 선분이 같은 시간 동안 쓸고 지나가는 면적은 항상 같다.
- 제3법칙(조화의 법칙) : 행성의 공전주기의 제곱은 궤도의 긴반지름의 세제곱에 비례한다.
법칙의 발견
케플러 제1법칙과 제2법칙은 티코 브라헤(1546-1601)의 방대하고 정밀한 화성 관측 자료에 근거하여 발견되었다. 티코 브라헤는 당대 최고의 정밀 관측 천문학자로서, 티코 사후 그의 자료를 물려받은 케플러는 화성의 관측 자료를 단순한 폐곡선으로 이루어진 태양 중심의 궤도에 집어넣기 위해 수 년 동안 씨름했다. 코페르니쿠스의 태양중심설을 굳게 믿고 있던 케플러는 지구를 포함한 각 행성의 궤도들이 고정된 태양을 기준으로 한 단순한 폐곡선으로 만들어진다고 추측했다. 즉 케플러의 목적은 지구에서 관측된 자료를 이용해 태양을 기준으로 한 화성의 궤도를 알아내는 것이었다. 그러나 지구에서는 천체의 각도만 측정될 뿐 천체까지의 거리는 측정되지 않기 때문에, 케플러의 작업은 다음과 같은 복잡한 단계를 거쳐 이루어졌다.
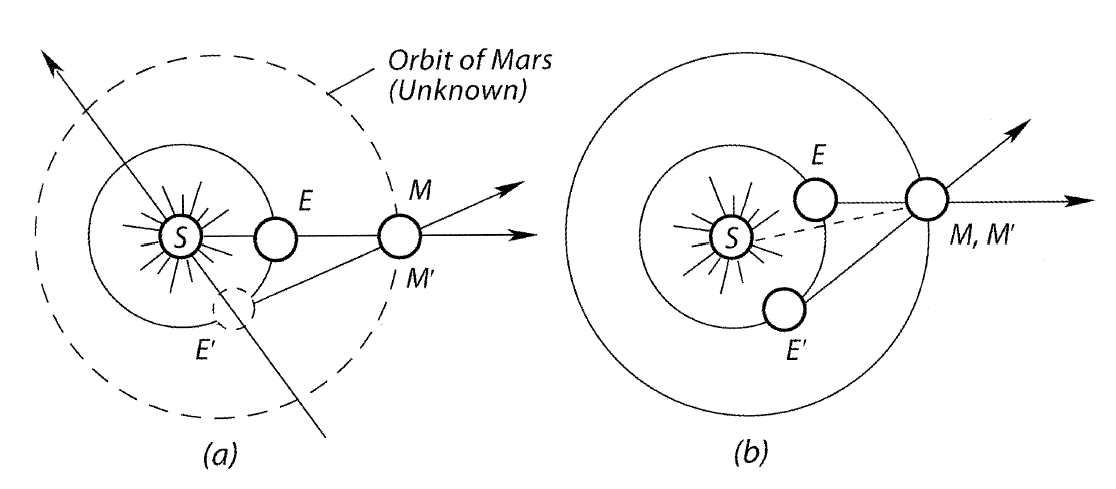
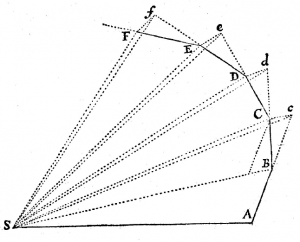
그림 1. (a) 화성의 궤도를 이용한 지구 궤도 확정, (b) 화성의 위치 확정
우선 케플러는 태양을 기준으로 한 지구의 궤도를 확정해야 했다(그림 1의 a). 태양을 기준으로 한 화성의 공전 주기는 687일로 측정되어 있었으며, 케플러는 화성이 687일마다 정확히 동일한 위치에 있을 것이라고 추측했다. 어느날 태양(S)과 지구(E)와 화성(M)이 일직선상에 놓였다고 하자. 그로부터 687일 후 화성(M')은 원래의 자리에 돌아올 것이며, 이때 지구(E')의 위치는 지구에서 측정된 태양의 각도와 화성의 각도를 통해 확정된다. 또다시 687일 후의 지구의 위치도 똑같은 방식으로 측정될 수 있으며, 이를 반복하면 지구의 궤도가 확정된다. 이렇게 확정된 지구의 궤도는 거의 완벽한 원으로 그려질 수 있었고, 그 중심은 태양에서 살짝 벗어나 있었다. 대신 공전 속도는 일정하지 않았다.
지구의 궤도를 확정한 후, 케플러는 화성의 위치들을 찍기 시작했다(그림 1의 b). 어느 날 지구(E)에서 화성이 특정한 방향에서 측정되었다고 해보자. 그러면 화성은 직선 EM 상에 존재해야 한다. 그로부터 687일 후 지구(E')에서 화성은 또 다른 방향에서 측정된다. 이때 화성은 직선 E'M' 상에 존재해야 한다. 그런데 태양을 기준으로 한 화성의 공전 주기는 687일이므로, 두 화성 M과 M'은 동일한 위치에 있어야 한다. 즉 화성의 위치는 EM과 E'M'의 교점으로 확정된다. 이와 같은 방식으로 구한 화성의 위치들을 모아 완성한 화성의 궤도는 원이 아니었다. 임의의 세 점을 지나는 원을 작도할 때마다 또 다른 한 점은 항상 원에서 이탈했기 때문이다. 즉, 티코가 남긴 자료의 작은 오차 범위를 고려할 때 그 궤도는 원으로 간주될 수 없었다. 화성의 궤도는 태양을 초점으로 하는 타원이었고, 이로써 타원 궤도의 법칙이 발견됐다.
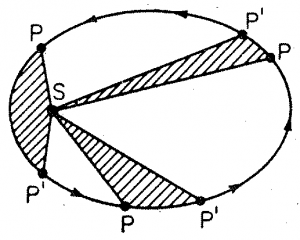
확정된 타원 궤도상에서 화성의 속도는 태양과의 거리에 의존했는데, 지구의 운동과 마찬가지로 근일점에서 가장 빠르고 원일점에서 가장 느렸다. 케플러는 행성을 돌려주는 태양의 힘이 거리에 반비례하여 행성에 도달한다고 가정함으로써 이를 설명하고자 했다. 그리고 그는 이 원초적인 생각을 티코의 관측 자료와 맞추는 과정에서는 ‘면적 속도 일정의 법칙’을 발견했다. 이 법칙에 따르면, 그림 2의 궤도에서 행성(P)과 태양(S)을 잇는 선분이 같은 시간 동안 쓸고 지나가는 면적(SPP′)은 항상 일정하다. 이러한 케플러의 이론은 티코의 행성 관측 자료를 오차 범위 내에서 설명할 수 있는 유일한 이론이었고, 이로써 ‘천구(orb)’는 ‘궤도(orbit)’로 완전히 대체되었다.
뉴턴의 증명
뉴턴은 원래 케플러의 제3법칙(조화의 법칙)과 행성의 원운동을 가정할 경우 태양의 인력이 거리의 제곱에 반비례할 것이라는 간단한 증명을 한 바 있다. 나중에 핼리가 방문하여 "거리의 제곱에 반비례하는 인력이 작용할 경우 물체의 궤도가 어떻게 되느냐?"는 질문을 받은 뉴턴은 완전한 증명에 착수한다. 간단히 요약하자면, 뉴턴은 구심력을 가정하여 케플러의 제2법칙(면적 속도 일정의 법칙)을 유도하고, 구심력에 의한 물체의 궤도가 타원일 경우(케플러의 제2법칙) 그 구심력의 크기가 거리의 제곱에 반비례함을 증명한다. 단 이러한 증명들은 기본적으로는 뉴턴의 운동 법칙  를 전제하고 있다.
를 전제하고 있다.
이 섹션의 증명은 『프린키피아』에서 사용된 뉴턴의 기하학적 증명 방식을 거의 그대로 따르고 있지만, 독자들의 이해를 위해 표현과 순서를 조정하였으며, 그 과정에서 뉴턴은 사용하지 않은
 와 같은 기호도 추가적으로 사용되었다는 점을 밝힌다.
와 같은 기호도 추가적으로 사용되었다는 점을 밝힌다.
케플러 제2법칙 : 면적 속도 일정의 법칙[1]
뉴턴의 가정에 따르면, 물체는 일정한 시간( ) 간격으로 (
) 간격으로 ( 등의 지점에서)
등의 지점에서)  방향의 순간적인 충격(크기는 상관이 없음)을 받으며, 충격을 받지 않는 동안에는 관성에 의해 등속 직선 운동을 한다. 또한 충격은 충격과 무관한 성분의 운동에는 영향을 주지 않으며, 충격과 동일한 방향의 성분의 운동만을 더해준다.
방향의 순간적인 충격(크기는 상관이 없음)을 받으며, 충격을 받지 않는 동안에는 관성에 의해 등속 직선 운동을 한다. 또한 충격은 충격과 무관한 성분의 운동에는 영향을 주지 않으며, 충격과 동일한 방향의 성분의 운동만을 더해준다.  로 각각 이동하는 데 걸린 시간을 모두 동일한
로 각각 이동하는 데 걸린 시간을 모두 동일한  로 두었을 때, 그 시간 동안
로 두었을 때, 그 시간 동안  와 물체 사이의 선분이 휩쓸고 지나간 면적은 각각
와 물체 사이의 선분이 휩쓸고 지나간 면적은 각각  등이 된다.
등이 된다.
 에서
에서  로 이동 중이던 물체가
로 이동 중이던 물체가  에서 충격을 받지 않았다면 물체는 직선 관성 운동에 의해 점선을 따라
에서 충격을 받지 않았다면 물체는 직선 관성 운동에 의해 점선을 따라  후에
후에  에 도착했을 것이다. 그러나
에 도착했을 것이다. 그러나  방향으로 받은 충격 때문에
방향으로 받은 충격 때문에  후 물체는
후 물체는  에 도착하게 된다(
에 도착하게 된다( [평행]). 왜냐하면
[평행]). 왜냐하면  방향으로 운동 중이던 물체에게 가해진
방향으로 운동 중이던 물체에게 가해진  방향의 충격은
방향의 충격은  방향의 운동에는 영향을 주지 않은 채
방향의 운동에는 영향을 주지 않은 채  방향(즉
방향(즉  방향)의 운동만을 더해주기 때문이다. 이때 다음과 같은 관계가 성립한다.
방향)의 운동만을 더해주기 때문이다. 이때 다음과 같은 관계가 성립한다.
 (
( [밑변의 길이 동일] & 삼각형의 높이 공유)
[밑변의 길이 동일] & 삼각형의 높이 공유) (
( 라는 밑변 공유 &
라는 밑변 공유 &  [삼각형의 높이 동일] )
[삼각형의 높이 동일] )
이어서  등에서
등에서  방향으로 받은 충격을 고려하면 아래와 같은 관계가 성립한다.
방향으로 받은 충격을 고려하면 아래와 같은 관계가 성립한다.

위의 관계는  를 극히 작은 크기로 줄이더라도 성립하게 되며, 이는 하나의 점 S로부터 '지속적으로' 힘을 받는 물체의 부드러운 곡선 궤도 운동에도 그대로 적용될 수 있다. 즉 임의의 물체
를 극히 작은 크기로 줄이더라도 성립하게 되며, 이는 하나의 점 S로부터 '지속적으로' 힘을 받는 물체의 부드러운 곡선 궤도 운동에도 그대로 적용될 수 있다. 즉 임의의 물체  가 일정한 점
가 일정한 점  로부터의 인력, 즉 구심력만을 받고 있을 경우 선분
로부터의 인력, 즉 구심력만을 받고 있을 경우 선분  가 같은 시간 동안 휩쓸고 지나가는 면적은 항상 동일하며, 이를 다르게 표현할 경우 그 면적은 시간에 비례한다. (주의할 점 : 이 법칙은 구심력의 크기와는 무관하게 성립한다.)
가 같은 시간 동안 휩쓸고 지나가는 면적은 항상 동일하며, 이를 다르게 표현할 경우 그 면적은 시간에 비례한다. (주의할 점 : 이 법칙은 구심력의 크기와는 무관하게 성립한다.)
케플러 제1법칙 : 타원 궤도의 법칙
뉴턴은 『프린키피아』 1권 제3장. 명제 11(문제 6)에서 "한 물체가 타원상을 공전한다고 했을 때, 타원의 초점으로 향하는 구심력의 법칙을 발견하다"는 문제를 제시하고, 그 답이 "거리의 제곱에 반비례하는 힘"이라는 것을 증명한다.[2] 이후 반대의 증명, 즉 거리의 제곱에 반비례하는 구심력이 작용할 때 물체의 궤도가 2차곡선의 형태가 된다는 증명도 완성한다.
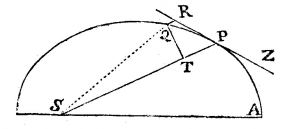
뉴턴의 구심력 법칙 : 점

에서 점

방향으로 작용한 구심 가속도

1단계. 점  에서 점
에서 점  방향으로 작용한 구심 가속도
방향으로 작용한 구심 가속도  의 증명.[3]
의 증명.[3]
 를 향한 구심력에 의해 궤도 운동을 하고 있는 물체를 가정하자. 물체가 점
를 향한 구심력에 의해 궤도 운동을 하고 있는 물체를 가정하자. 물체가 점  를 지나는 순간의 접선
를 지나는 순간의 접선  를 그린 후, 접선 위의 한 점
를 그린 후, 접선 위의 한 점  에서
에서  에 평행한 직선을 그려 타원과 만나는 점을
에 평행한 직선을 그려 타원과 만나는 점을  라고 하자.
라고 하자.  에서
에서  까지의 아주 짧은 시간
까지의 아주 짧은 시간  동안은 물체가
동안은 물체가  방향의 일정한 힘을 받아 등가속도로 운동한다고 가정하면, 아래의 식이 성립한다(단,
방향의 일정한 힘을 받아 등가속도로 운동한다고 가정하면, 아래의 식이 성립한다(단,  와
와  는 물체가 점
는 물체가 점  를 지날 때의 속도와 구심 가속도).
를 지날 때의 속도와 구심 가속도).
 (
( 방향으로는 등속 운동)
방향으로는 등속 운동) [4] (
[4] ( 방향으로는 초기 속도가 0인 등가속도 운동)
방향으로는 초기 속도가 0인 등가속도 운동)
- 그런데 구심력에 의해 움직이는 물체가 훓고 지나가는 면적은 시간에 비례하므로,
 (단,
(단,  ).
).
- 따라서 구심 가속도
 .
.
2단계.  의 증명.
의 증명.
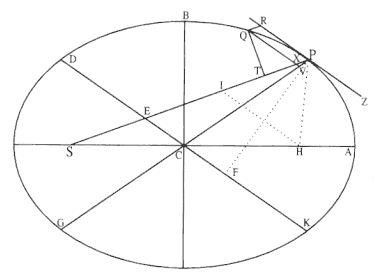
케플러 제1법칙으로부터 역제곱 법칙의 도출
 는 타원의 초점이며,
는 타원의 초점이며,  는
는  에서의 접선이다. 타원의 중심
에서의 접선이다. 타원의 중심  에서
에서  에 평행한
에 평행한  를 그려
를 그려  와 만나는 교점을
와 만나는 교점을  라고 한다. 그리고 타원의 또 하나의 초점
라고 한다. 그리고 타원의 또 하나의 초점  에서부터
에서부터  에 평행하게
에 평행하게  를 그리면,
를 그리면,  와
와  는 타원의 두 초점이므로
는 타원의 두 초점이므로  이고, 또한
이고, 또한  이므로,
이므로,

- 따라서

- 그런데 타원의 성질에 의해
 이고,
이고,  이므로,
이므로,


- 또한 타원의 장축
 이므로,
이므로,
 .
.
3단계.  의 증명.
의 증명.
 에 평행하게
에 평행하게  를 그리고(
를 그리고( 는
는  와의 교점,
와의 교점,  는
는  와의 교점),
와의 교점),  에서
에서  에 수선
에 수선  를 내리자. 타원의 긴 반지름과 짧은 반지름의 길이를 각각
를 내리자. 타원의 긴 반지름과 짧은 반지름의 길이를 각각  와
와  라고 할 때, (N2)를 고려하면 아래의 관계들이 성립힌다.
라고 할 때, (N2)를 고려하면 아래의 관계들이 성립힌다.


- 그리고 타원에 외접한 평행사변형의 넓이는 모두 동일하므로,

- (1)에 의해

- (2)와 (3)에 의해

- (5)의 제곱을 (4)로 나누어 극한을 취하면,

- 그런데
 와
와  를 각각 타원의 긴 반지름과 짧은 반지름으로 삼은 좌표계에서 타원상의 임의의 한 점
를 각각 타원의 긴 반지름과 짧은 반지름으로 삼은 좌표계에서 타원상의 임의의 한 점  는 아래의 성질을 만족한다.
는 아래의 성질을 만족한다.


- (6)의 식에 (7)을 적용하면,

4단계.  의 증명.
의 증명.
- (N1)과 (N3)를 결합하면 구심 가속도

- 구심력
 이므로
이므로  이 성립한다.
이 성립한다.
현대적인 증명
물체에 만유인력의 법칙(거리의 제곱에 반비례하는 구심력)이 작용할 때 물체가 가지게 되는 궤도의 특성을 도출할 것이다.
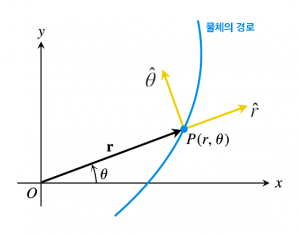
극좌표계의 두 단위벡터

과

.
구심력의 중심을 기준으로 한 물체의 위치 벡터

을 다음과 같은 극좌표로 표현해보자.
 (단,
(단,  은
은  방향의 단위 벡터).
방향의 단위 벡터).
그러면 직교 단위 벡터  과
과  사이에는 다음의 두 가지 관계가 성립한다.
사이에는 다음의 두 가지 관계가 성립한다.

이러한 관계를 이용하여  을 시간
을 시간  에 대해 미분하면,
에 대해 미분하면,

이를 시간  에 대해 한 번 더 미분하면,
에 대해 한 번 더 미분하면,
 .
.
이제 만유인력의 법칙을 가정하면

이는 아래와 같은 두 개의 식으로 분해된다.

(M2)의 미분방정식은 아래와 같이 풀린다.


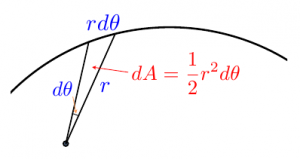
궤도 운동을 하는 점과 중심 사이를 잇는 선분이 훑고 지나가는 면적

(M3)를 이용하여 궤도 운동을 하는 물체와 중심을 잇는 선분이 단위 시간마다 훑고 지나가는 면적  를 구하면
를 구하면

이로써 구심력에 의해 움직이는 물체가 동일한 시간 동안 훑고 지나가는 면적이 항상 일정하다는 케플러 제2법칙이 증명되었다.
이제 (M1)을 풀 차례이다. 우선  로 치환해보자. (M3)를 활용하면
로 치환해보자. (M3)를 활용하면  과
과  은 아래와 같이 변환된다.
은 아래와 같이 변환된다.


(M3)와 (M4)를 활용하여 (M1)을 변환하면,


이 미분방정식을 풀면 아래의 해가 나온다.
 (단,
(단,  와
와  는 상수)
는 상수)
이 해를  로 치환하면 아래와 같은 해로 변환된다.
로 치환하면 아래와 같은 해로 변환된다.
 (단,
(단,  와
와  는 상수)
는 상수)
이 관계식은 물체의 궤도가 원뿔곡선임을 함축하며, 구체적인 형태는 이심률  의 값에 따라 달라진다.
의 값에 따라 달라진다.

 일 때, (K1)이 타원이라는 점은 다음을 통해 알 수 있다.
일 때, (K1)이 타원이라는 점은 다음을 통해 알 수 있다.
단순화를 위해  이 되는
이 되는  를 이용하면 (K1)은 아래의 식으로 변환된다.
를 이용하면 (K1)은 아래의 식으로 변환된다.

이 관계식은 원점과  을 두 개의 초점으로 가지고 장축이
을 두 개의 초점으로 가지고 장축이  , 이심률이
, 이심률이  , 단축이
, 단축이  인 아래와 같은 타원을 만들어낸다.
인 아래와 같은 타원을 만들어낸다.
이로써 거리의 제곱에 반비례하는 구심력을 받는 물체가 ( 의 조건에서) 케플러 제1법칙에 따라 타원 궤도를 돈다는 것이 증명되었다.
의 조건에서) 케플러 제1법칙에 따라 타원 궤도를 돈다는 것이 증명되었다.
주석
- ↑ 뉴턴은 『프린키피아』 1권 2장, 명제 1(정리 1)에서 케플러 제2법칙을 다루고 있다. 홍성욱 편역, 『과학고전선집』 (서울대학교출판문화원, 2006), 386쪽.
- ↑ 홍성욱 편역, 과학고전선집 (서울대학교출판문화원, 2006), 407쪽.
- ↑ 이 부분의 증명은 ⟪프린키피아⟫ 1권 명제 6. 정리 5에 해당한다. 홍성욱 편역, 과학고전선집 (서울대학교출판문화원, 2006), 397쪽.
- ↑ 이 두 식은 등가속도 운동 공식
 과 같은 형태의 식이다. 사실 이 등가속도 공식은 비등가속 운동을 하는 물체의 위치 벡터에 대한 테일러 전개에서 3차 도함수 이하를 제거한 형태이다.
과 같은 형태의 식이다. 사실 이 등가속도 공식은 비등가속 운동을 하는 물체의 위치 벡터에 대한 테일러 전개에서 3차 도함수 이하를 제거한 형태이다.  를 기준으로 한 물체의 위치 벡터
를 기준으로 한 물체의 위치 벡터  를 시간
를 시간  에 관한 함수
에 관한 함수  로 나타낸 후(단, 점
로 나타낸 후(단, 점  에서
에서  ), 이를 전개하면,
), 이를 전개하면,  가 성립한다.
가 성립한다.
관련 항목